Runda 9 a atras 112 participanti. Dintre acestia, 103 au trimis cel putin o sursa, iar 88 de concurenti au rezolvat corect cel putin o problema. Setul de probleme ales a fost unul mai usor decat in rundele precedente. Spre deosebire de ultimele 3 runde, unde concurentii au putut rezolva maxim 3 probleme in timp de concurs, in runda asta 5 concurenti au rezolvat corect toate problemele. Cei cinci: 
Serviciu
Aceasta a fost problema simpla a setului. 86 concurenti au trimis o sursa corecta in timpul concursului la ea. De asemenea, cea mai rapida submisie corecta a venit dupa doar 4 minute de la inceperea rundei, apartinand castigatorului premiului IXIA si al rundei
Pentru a rezolva problema, trebuie sa aflam intai, pentru fiecare dintre cei N locatari, distanta minima dintre birou si locuinta. Distanta maxima parcursa va fi maximul acestor N valori calculate.
Cum calculam distanta minima dintre 2 blocuri? Fie x coordonata locuintei si y coordonata biroului. Putem presupune ca x < y. In cazul in care x > y, putem interschimba valorile lui x si y. Interschimbarea nu schimba rezultatul, deoarece distanta minima de la locuinta la birou este aceeasi cu distanta minima de la birou la locuinta.
Acum locatarul nostru trebuie sa se plimbe pe conturul cercului (pornind din x si ajungand in y). El se poate plimba fie in sens trigonometric (reprezentat cu rosu in desenul din stanga) fie in sens orar (reprezentat cu albastru). Nu are niciun rost ca locatarul sa-si aleaga un sens de deplasare si apoi, undeva in drumul sau sa si-l schimbe. Practic schimbarea sensului va anula ce a mers el inainte, crescand distanta parcursa de el inutil. Asadar, distanta minima va fi minimul dintre distanta obtinuta daca ar alege sensul rosu si distanta obtinuta daca ar alege sensul albastru.
Vom calcula concret distantele pentru cele doua sensuri. Sa presupunem ca locatarul trece prin cladirile x, x1, x2, ..., xn, y. Distanta parcursa va fi dist(x, x1) + dist(x1, x2) + ... + dist(xn-1, xn) + dist(xn, y). Dar distanta dintre oricare 2 constructii consecutive este 1, deci distanta totala parcursa este defapt numarul de cladiri diferite de x prin care trece locatarul.
Pentru sensul rosu, cum x < y, locatarul va trece intotdeauna prin cladirile x + 1, x + 2, ..., y - 1, y. Numarul acestora este y - (x + 1) + 1 = y - x. Pentru sensul albastru, locatarul va trece prin cladirile x - 1, x - 2, ..., 2, 1, 2 * N, 2 * N - 1, ..., y + 1, y. Pentru a calcula numarul de cladiri pe care le parcurge locatarul in acest caz, vom calcula intai cata distanta trebuie sa parcurga pentru a ajunge la cladirea 2 * N, dupa aceea ce distanta trebuie sa mai parcurga de la cladirea 2 * N la cladirea y. Pentru a ajunge la cladirea 2 * N, locatarul trebuie sa treaca pe langa cladirile x - 1, x - 2, ..., 1 si 2 * N.
Pentru a ajunge la coordonata 1, el trebuie sa parcurga x - 1 cladiri, iar pentru a ajunge la de la 1 la 2 * N mai trebuie sa mearga 1 unitate de distanta. Asadar, distanta dintre x si 2 * N este x. Acum, ppornind din 2 * N, locatarul trebuie sa ajunga in y. El parcurge cladirile 2 * N - 1, 2 * N - 2, ..., y + 1, y. In total, aceste cladiri sunt in numar de 2 * N - 1 - y + 1 = 2 * N - y. Deci distanta totala pentru sensul albastru este x + 2 * N - y. Evident, distanta minima dintre cladirea x si cladirea y va fi acum min(y - x, x + 2 * N - y).
Formula de baza folosita pentru rezolvarea problemei a fost ca numarul de numere dintr-o multime {A, A + 1, A + 2, .., B - 1, B} este B - A + 1. Complexitatea algoritmului este O(N) timp si O(1) memorie.
Traseu2
Si aceasta problema a fost una simpla a setului, dar mai grea decat Serviciu. Problema era una de implementare. 47 concurenti au reusit sa duca la bun sfarit problema in timpul concursului. Pentru a obtine un scor bun, codul problemei trebuia simplificat pe cat posibil, fara a intra in complicatii inutile. Lui 
Primul lucru de facut este citirea matricii. Din pacate, aceasta nu se poate citi "clasic" (citind N * M numere intregi), deoarece ea contine si caractere "#". Astfel, va trebui sa citim ca sir de caractere fiecare dintre cele N * M numere, apoi sa le convertim in intregi. In cazul in care este vorba de caracterul "#", vom pune conventional valoarea -1. Pentru a citi doar un singur numar (sub forma de sir de caractere), se pot folosi functii precum scanf sau cin (pentru streamuri). Aceste functii citesc din fisier pana intalnesc un caracter alb (spatiu sau enter), apoi se opresc. Alternativ, se poate citi textul linie cu linie (in loc de numar cu numar) si apoi sa se parseze valorile de pe fiecare linie citita.
O restrictie importanta a problemei este ca fiecare element din matrice este diferit. Astfel, fiecarei valori din matrice (prin valoare nu am inclus elementele -1) ii corespunde o pozitie unica in matrice (prin pozitie ma refer la linia si coloana elementului in matrice). Mai formal, fiecare valoare x poate fi exprimata in mod unic sub forma unei perechi (i, j), astfel incat pe linia i si coloana j din matrice sa se afle valoarea x.
Sortam in ordine crescatoare valorile (din nou, ignoram valorile de -1). Acum, daca in loc sa scriem valorile in ordine crescatoare, am scrie pozitiile corespunzatoare fiecarei valori, am obtine un posibil drum. Daca acest drum nu e valid, nu va exista niciun alt drum care sa fie. Demonstratia acestei proprietati vine destul de simplu. Exista un singur mod de a sorta valorile, iar fiecarei valori ii corespunde o singura pozitie. Astfel, poate exista cel mult un drum.
Tot ce mai ramane de facut este sa verificam daca drumul ales este valid. Un drum este valid cand orice 2 elemente consecutive din el sunt vecine in matrice. Fie (x0, y0) o pozitie oarecare si (x1, y1) pozitia urmatoare din drum. Daca (x1, y1) nu este vecin al lui (x0, y0), drumul nu este valid. Cum vedem daca 2 pozitii (x0, y0) si (x1, y1) sunt vecine? O prima idee ar fi sa generam toti cei 8 vecini ai lui (x0, y0) ssi sa verificam daca (x1, y1) apare printre ei. O abordare mai rapida de scris ar fi sa observam ca (x0, y0) si (x1, y1) sunt vecine daca si numai daca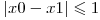 
si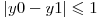 
. Lasam demonstratia acestei proprietati ca tema cititorului.
O sursa care implementeaza ideea de mai sus este a lui Ciprian Olariu.
Intersort
15 concurenti au reusit sa rezolve problema in timpul rundei. Totusi, doar 3 dintre ei au reusit s-o rezolve cu un punctaj mai mare de 50 (punctajul minim acordat pe o solutie care trece toate testele). Problema era una de idee, care necesita cunostinte elementare de combinatorica. In general, scorurile sunt asa mici din cauza trimiterii mai multor submisii. Unii concurenti au implementat solutii gresite, care mergeau numai pe cazuri particulare, fara a demonstra ca functioneaza pe caz general. Testele feedback au aratat ca submisia nu e buna si concurentul a trebuit s-o ia de la capat. Alta cauza a resubmisiilor a fost testul 7, fiind un caz particular. De exemplu, acest test l-a facut pe
Pentru a rezolva problema initiala, propun sa rezolvam o versiune simplificata a ei. Sa presupunem ca orice interschimbare are costul 1. Care este costul minim ca sa sortam permutarea? Vom descompune permutarea in cicli. Oricare 2 cicli sunt disjuncti (un element apartine unui singur ciclu), deci costul sortarii permutarii este egal cu suma costurilor sortarii fiecarui ciclu.
Fie x1, x2, ..., xn elementele ciclului curent (adica perm(x1) = x2, perm(x2) = x3, ..., perm(xn-1) = xn, perm(xn) = x1). Costul sortarii acestui ciclu este n - 1. De ce? Sa presupunem ca intai vreau sa am grija ca elementul xn sa fie pe pozitia corecta. (perm(xn) = xn). Prin swap(x, y) inteleg ca voi interschimba valorile perm(x) si perm(y). Stiu ca perm(xn-1) = xn, deci daca fac swap(xn-1, xn), perm(xn) = xn si perm(xn-1) = x1. In continuare, vreau sa mai fac un swap astfel incat perm(xn-1) = xn-1. Stiu ca perm(xn-2) = xn-1. Daca fac swap(xn-2, xn-1), perm(xn-1) va fi xn-1 si perm(xn-2) = x1. Daca fac operatiile swap(xn, xn-1), swap(xn-1, xn-2), swap(xn-2, xn-3), .., swap(x3, x2), swap(x2, x1) voi sorta tot ciclul curent, folosind doar n - 1 operatii. Las ca tema pentru acasa demonstratia ca acest numar este minim pentru a sorta un ciclu. Mai jos am considerat un exemplu de sortare a unui ciclu dupa metoda descrisa.
![\begin{pmatrix}
1 & 2 &3 & 4 & 5\\
5 & 3 &4 & 1 & 2\
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
5 & 3 & 1 & 4 & 2
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
5 & 1 & 3 &4 & 2
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 &3 & 4 & 5\\
5 & 2 & 3 & 4 & 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 &3 & 4 &5 \\
1 & 2 & 3 & 4 & 5
\end{pmatrix}](https://www.infoarena.ro/static/images/latex/6fd18dcc355af08f780bc2f255cda574_10.50012pt.gif "\begin{pmatrix}
1 & 2 &3 & 4 & 5\\
5 & 3 &4 & 1 & 2\
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
5 & 3 & 1 & 4 & 2
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
5 & 1 & 3 &4 & 2
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 &3 & 4 & 5\\
5 & 2 & 3 & 4 & 1
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 &3 & 4 &5 \\
1 & 2 & 3 & 4 & 5
\end{pmatrix}")
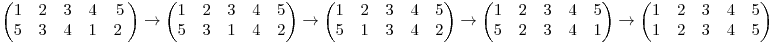
In imagine avem x1 = 1, x2 = 5, x3 = 2, x4 = 3, x5 = 4.
Ce legatura are problema de mai sus cu problema noastra originala? Daca fac interschimbari numai cu elementul 1, problema se reduce la cea de sus. (costul unei operatii este min(1, x) = 1). Vom considera 4 cazuri diferite (care acopera defapt toata problema):
Caz 1. Lungimea ciclului curent este 1 (punct fix). In acest caz, ciclul este deja sortat, costul sortarii lui fiind 0.
Caz 2. Consideram un ciclu x1, x2, ..., xn, in care x1 = 1. Costul sortarii acestui ciclu este n - 1 (aceasta este exact problema de mai sus, deoarece la fiecare pas voi face interschimbari cu elementul 1).
Caz 3. (Caz particular, corespunzator testului 7) Avem un ciclu x1, x2, iar x1 = 2. Voi face pur si simplu swap(x1, x2), avand costul 2.
Caz 4. Avem un ciclu x1, x2, ..., xn si x1 este diferit de 1. Costul sortarii acestui ciclu este n + 1. Sa presupunem ca perm(1) = 1 (adica am rezolvat intai cazul 2). Fac intai swap(1, xn). Apoi fac algoritmul de la cazul 2. (in total n - 1 pasi). Apoi fac swap(1, x1). Astfel, sunt in total n + 1 operatii. Pentru a intelege mai bine, am mai luat un exemplu mai jos. De remarcat ca daca am aplica cazul acesta si pentru rezolvarea cazului 3, am obtine costul 3, care este incorect (cum am aratat mai sus, pot sorta cazul 3 numai cu costul 2). Pentru n >= 3, acest caz sorteaza optim, indiferent de permutare.
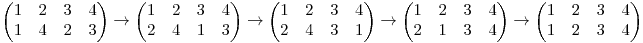
Mai trebuie mentionat ca complexitatea algoritmului este data de complexitatea descompunerii in cicluri, care se face in O(N).
Petrecere2
Aceasta a fost problema grea a setului. Ea a fost rezolvata corect doar de 8 concurenti. Cu toate astea, problema nu era atat de grea odata ce se faceau niste observatii cheie. Codarea solutiei trebuia facuta cat mai simplu posibil si aici, altfel puteau aparea buguri care sa compromita toata problema.
Pentru inceput, putem considera fiecare persoana un nod intr-un graf si fiecare relatie o muchie neorientata in graf. Daca tipul relatiei era 0, vom numi muchia muchie de tip 0, altfel muchia va fi de tip 1. Problema cere o colorare a grafului. Vom spune ca un nod are culoare alba daca persoana corespunzatoare lui vine la petrecere si neagra daca nu vine. In exemplu, nodurile 1 si 2 sunt albe si nodul 3 este negru.
Observatia cheie care rezolva problema este ca daca stiu culoarea unui nod x pot afla culoarea tuturor nodurilor din componenta conexa a lui x. Pentru asta sa analizam mai atent tipul muchiilor:
- O muchie de tip 0 dintre doua noduri x si y arata ca x si y au aceeasi culoare. Sa presupunem ca x este alb. Persoana X ar veni la petrecere numai daca toate persoanele cu care se afla in relatii de tip 0 ar veni. Implicit, persoana Y trebuie sa vina, deci culoarea lui Y este tot alb. Acum, daca x ar avea culoarea neagra, Y este obligat sa aiba culoarea neagra si el. Rationamentul este asemanator: Y vine la petrecere doar daca vine si X, cum X nu vine, nici Y nu vine.
- O muchie de tip 1 dintre doua noduri x si y arata ca x si y au culori diferite. Presupun si aici ca x e alb. Daca x vine la petrecere, y nu va veni (conform definitiei relatiei de tip 1). De asemenea, daca x nu vine, y trebuie sa vina ("Paftenie mai stie ca daca 2 prieteni de-ai sai se afla in relatia de dusmanie, trebuie neaparat sa il invite pe unul din ei altfel vor fi amandoi suparati.")
De aici se contureaza ideea algoritmului. Pornim dintr-un nod arbitrar, presupunem ca el are culoare alba. Apoi aflam toate nodurile din componenta conexa a nodului ales (se poate face prin parcurgeri precum BFS si DFS) si pentru fiecare nod y descoperit dintr-un nod x vom actualiza culoarea lui y in functie de culoarea lui x si tipul muchiei dintre x si y. Daca nodul ales arbitrar ar avea culoarea neagra, tot ce s-ar intampla ar fi ca nodurile albe din componenta conexa sa devina negre si nodurile negre sa devina albe. (Las tema de gandire pentru cititori demonstrarea acestei proprietati). Astfel, e nevoie sa parcurg graful doar pentru culoarea alba initiala, pentru culoarea neagra se poate afla prin contrast.
Mai departe, calculez pentru nodul ales arbitrar mai sus daca e mai bine sa-l colorez in alb sau negru. Evident, o colorare se considera buna cand aduce un numar maxim de noduri albe. Fie N = nr de noduri din componenta conexa curenta si white = numarul de noduri albe. Pentru o colorare pornind cu culoarea initiala alba, numarul de noduri albe va fi white. Daca am porni cu negru initial, numarul de noduri negre ar fi white si numarul de noduri albe ce mai ramane din cele N noduri ale componentei (N - white). Astfel, pentru o componenta conexa, la solutie se va adauga valoare max(white, N - white). Dupa aceea componenta conexa se elimina si algoritmul se reia.
Timpul de rulare al algoritmului este O(N + M). Practic, eliminarea unui nod se poate face in O(1) daca il marchez ca fiind vizitat, iar in timpul unei parcurgeri consider numai nodurile nevizitate
