Revizia anterioară Revizia următoare
Probleme cu numere lipsa si nu numai ...
(Categoria Diverse, autor Cosmin Negruseri)
Problema 1 ( interviu Microsoft )
Se dau n-1 numere distincte de la 1 la n, sa se dea un algoritm cat mai eficient care sa determine numarul lipsa.
Rezolvare
Prima rezolvare ce ne poate veni in minte este aceea ca pentru fiecare numar de la 1 la n sa verificam daca numarul curent nu exista in sir prin o parcurgere. Un astfel de algoritm are complexitatea 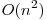 si vom vedea mai departe ca putem obtine solutii mult mai bune.
si vom vedea mai departe ca putem obtine solutii mult mai bune.
O rezolvare triviala ar fi sa sortam cu metoda noastra preferata numerele si sa le parcurgem pentru a vedea cand a[i] != i. Aceasta rezolvare are complexitatea 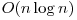 .
.
O rezolvare mai eficienta poate fi data urmarind ideea algoritmului Quick Sort. Putem imparti numerele in doua multimi, una in care vom pune mumerele mai mici sau egale cu n/2, iar in cealalta numerele mai mari decat n/2. Acum vom sti daca numarul lipsa este mai mic sau egal cu n/2 sau mai mare ca n/2, dupa numarul de elemente din fiecare lista. Astfel in 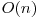 pasi am redus problema la jumatate. Daca avem
pasi am redus problema la jumatate. Daca avem 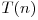 timpul de executie al acestui algoritm, atunci
timpul de executie al acestui algoritm, atunci 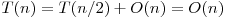 . Deci algoritmul este liniar, si foloseste memorie
. Deci algoritmul este liniar, si foloseste memorie 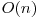 ignorand memoria consumata de sirul de numere
ignorand memoria consumata de sirul de numere 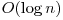 pentru stiva din algoritmul divide et impera.
pentru stiva din algoritmul divide et impera.
O alta idee este aceea de a folosi un tabel de dispersie sau un sir de valori booleene care va folosi memorie suplimentara 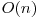 , iar daca folosim biti reducem memoria suplimentara la
, iar daca folosim biti reducem memoria suplimentara la 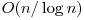 .
.
O rezolvare eleganta se foloseste de proprietatea ca suma numerelor naturale de la 1 la n este n(n+1)/2, iar suma numerelor o putem afla prin o parcurgere. Acum determinarea numarului lipsa se face prin scaderea din suma numerelor de la 1 la n a sumei numerelor noastre. Aceasta solutie are complexitatea 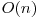 ca timp si
ca timp si 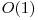 ca memorie folosita.
ca memorie folosita.
Daca n este destul de mare, s-ar putea ca n(n+1)/2 sa depaseasca domeniul de reprezentare al intregilor de pe calculatorul nostru si ar trebui sa implementam operatii cu numere mari ca solutia anterioara sa produca rezultatul corect. O rezolvare ce nu are aceasta problema se foloseste de operatia xor si de proprietatile ei 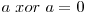 si
si 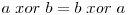 . Vom face suma xor a numerelor
. Vom face suma xor a numerelor ![a[i] \hspace{1mm} xor \hspace{1mm} i a[i] \hspace{1mm} xor \hspace{1mm} i](https://www.infoarena.ro/static/images/latex/5fdfb51ad27bce22c4ae6ea198dc973e_3.5pt.gif) cu
cu 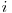 de la
de la  la
la 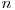 :
:
![S = a[1] \hspace{1mm} xor \hspace{1mm} 1 \hspace{1mm} xor \hspace{1mm} a[2] \hspace{1mm} xor \hspace{1mm} 2 \hspace{1mm} xor \hspace{1mm} ... \hspace{1mm} xor \hspace{1mm} a[n] \hspace{1mm} xor \hspace{1mm} n S = a[1] \hspace{1mm} xor \hspace{1mm} 1 \hspace{1mm} xor \hspace{1mm} a[2] \hspace{1mm} xor \hspace{1mm} 2 \hspace{1mm} xor \hspace{1mm} ... \hspace{1mm} xor \hspace{1mm} a[n] \hspace{1mm} xor \hspace{1mm} n](https://www.infoarena.ro/static/images/latex/fa788db1be90c878c1e7081db6e901ce_3.5pt.gif)
Astfel fiecare numar care apare in sir va fi in suma de doua ori si va fi anulat, iar pentru numarul lipsa, in suma va aparea doar indicele lui, care este si valoarea finala a sumei. Solutia are compexitatea 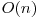 ca timp si
ca timp si 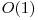 ca spatiu.
ca spatiu.
Problema 2 ( interviu Microsoft )
Se da un sir de n+1 numere de la 1 la n in care unul se repeta, iar restul sunt distincte. Sa se dea un algoritm cat mai eficient care sa determine numarul ce se repeta.
Rezolvare
Evident, abordarile de la problema anterioara se aplica si aici.
Problema 3 ( lot 1999, interviu Microsoft )
Se da o lista inlantuita prin primul ei element. Se cere un algoritm cat mai eficient care sa determine daca lista are sau nu ciclu.
Rezolvare
Fie n numarul total de elemente ale listei. O solutie in 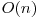 timp si
timp si 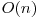 memorie ar fi sa parcurgem lista si sa adaugam pe rand elementele listei unui tabel de dispersie. Cand am introdus acelasi element de doua ori in lista este evident ca am gasit un ciclu. O metoda folosita de unii concurenti a fost parcurgerea listei pe o perioada de timp determinata, de exemplu timpul de executie fixat in problema. Acum sunt sanse mari ca daca nu am ajuns la capatul listei aceasta sa aiba ciclu.
memorie ar fi sa parcurgem lista si sa adaugam pe rand elementele listei unui tabel de dispersie. Cand am introdus acelasi element de doua ori in lista este evident ca am gasit un ciclu. O metoda folosita de unii concurenti a fost parcurgerea listei pe o perioada de timp determinata, de exemplu timpul de executie fixat in problema. Acum sunt sanse mari ca daca nu am ajuns la capatul listei aceasta sa aiba ciclu.
Exista un algoritm mai elegant ce foloseste memorie suplimentara 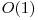 si este liniar. Acest algoritm se numeste Algoritmul lui Floyd de detectie a ciclului intr-o lista. O aplicatie importanta a lui este Algoritmul Pollard
si este liniar. Acest algoritm se numeste Algoritmul lui Floyd de detectie a ciclului intr-o lista. O aplicatie importanta a lui este Algoritmul Pollard 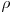 , folosit pentru factorizarea intregilor cu multe cifre. Algoritmul foloseste doi pointeri a si b, unde a se misca de doua ori mai repede decat b in lista, de aceea se mai numeste si Algoritmul iepurelui si testoasei.
, folosit pentru factorizarea intregilor cu multe cifre. Algoritmul foloseste doi pointeri a si b, unde a se misca de doua ori mai repede decat b in lista, de aceea se mai numeste si Algoritmul iepurelui si testoasei.
Reprezentarea grafica seamana cu litera greceasca 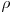 . Notam lungimea lantului cu
. Notam lungimea lantului cu 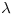 si lungimea ciclului cu
si lungimea ciclului cu 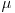 .
.
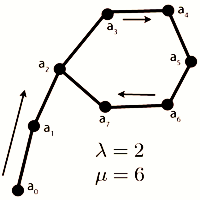
a = b = cap
repeta
a = a.next.next
b = a.next
cat timp (a!=b)Cand a si b sunt amandoi in ciclu, a il va ajunge din nou pe b. Puteti vedea exact cum prin analiza cazurilor in care lungimea ciclului e para sau impara. In exemplul desenat, dupa sase iteratii cei doi pointeri vor indica acelasi element.
Pentru determinarea lungimii ciclului se mai poate face o parcurgere in care doar un pointer se misca. Acum dupa ce stim lungimea 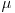 a ciclului putem afla si lungimea
a ciclului putem afla si lungimea 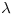 a lantului astfel: luam un pointer la inceputul listei si al doilea care a facut deja
a lantului astfel: luam un pointer la inceputul listei si al doilea care a facut deja 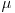 pasi in lista. Acum ii miscam pe cei doi cu aceeasi viteza. Dupa
pasi in lista. Acum ii miscam pe cei doi cu aceeasi viteza. Dupa 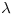 pasi cei doi pointeri vor fi egali. Astfel am obtinut o rezolvare liniara.
pasi cei doi pointeri vor fi egali. Astfel am obtinut o rezolvare liniara.
Problema 4 ( IBM Research: Ponder This )
Un sir ce poate fi numai citit, de lungime n contine numere intregi din multimea {1, 2, ..., n-1}. Folosind principiul lui Dirichlet deducem ca cel putin un element se repeta. Gasiti un algoritm liniar care afiseaza o valoare ce se repeta folosind memorie suplimentara constanta si nemodificand la nici un pas vreun element din sir.
Rezolvare
Aici nu merge solutia cu suma xor de la problemele 1 si 2 pentru ca numerele pot fi repetate oricum si nu putem folosi relatiile obtinute cu ajutorul lor pentru a determina un numar care se repeta.
Daca toate elementele din sir ar fi distincte, atunci sirul ar avea structura unei permutari. Cum ele nu sunt neaparat distincte ne vine ideea de a vedea care este diferenta intre un asemenea sir si o permutare. Astfel vom folosi idei care apar la permutari, cum ar fi ciclurile permutarilor. Fiecare element din sirul nostru indica inspre altul, deci ne putem gandi la sirul nostru ca un graf orientat in care arcele sunt (i, a[i]). De exemplu putem face urmatoarea reprezentare pentru sirul 3, 2, 1, 3, 4:
