Revizia anterioară Revizia următoare
Probleme cu numere lipsa si nu numai ...
Intră aici dacă doreşti să scrii articole sau află cum te poţi implica în celelalte proiecte infoarena! |
(Categoria Diverse, autor Cosmin Negruseri)
- Cuprins
- Problema 1 ( interviu Microsoft )
- Problema 2 ( interviu Microsoft )
- Problema 3 ( interviu Microsoft, lot 1999 )
- Problema 4 ( IBM Research: Ponder This )
- Problema 5
- Problema 6 ( interviu Microsoft )
- Problema 7
- Problema 8
- Problema 9
- Problema 10 ( el judge)
- Problema 11 ( Info-Oltenia 2005, clasa a IX-a)
- Bibliografie
Problema 1 ( interviu Microsoft )
Se dau n-1 numere distincte de la 1 la n, sa se dea un algoritm cat mai eficient care sa determine numarul lipsa.
Rezolvare
Prima rezolvare ce ne poate veni in minte este aceea de a verifica daca fiecare numar 1 -> n este prezent in sirul nostru, printr-o parcurgere (acest algoritm are complexitatea O(n2) ). O alta rezolvare triviala ar fi sa sortam numerele si sa determinam prin parcurgere numarul i pentru care a[i] != i (pentru sortari rapide algoritmul are complexitatea O(n log n) ).
O rezolvare mai eficienta poate fi data folosind Divide et Impera. Putem imparti numerele in doua multimi, una in care vom pune mumerele mai mici sau egale cu n/2, iar in cealalta restul. Acum vom sti din care din cele doua multimi lipseste numarul, dupa numarul de elemente al acestora. Considerand T(n) timpul de executie al algoritmului, atunci complexitatea devine T(n) = T(n/2) + O(n) = O(n). Deci algoritmul este liniar, si foloseste memorie O(n), ignorand memoria consumata de stiva din algoritmul Divide et Impera ( O(log n) ). O alta idee este de a folosi un tabel de dispersie sau un sir de valori booleene care va folosi memorie suplimentara O(n) (poate fi redusa la O(n/log n) daca se lucreaza pe biti).
O rezolvare eleganta se foloseste de proprietatea ca suma numerelor naturale de la 1 la n este n(n + 1)/2. Numarul lipsa este egal cu diferenta dintre n(n + 1 )/2 si suma numerelor noastre. Aceasta solutie are complexitatea O(n) (parcurgem sirul pentru a determina suma) ca timp si O(1) ca memorie. Daca n este destul de mare, s-ar putea ca n(n+1)/2 sa depaseasca domeniul de reprezentare al intregilor, rezultand in necesitatea implementarii operatiilor cu numere mari. Pentru a evita acest lucru folosim operatia xor (notata prin ∧ ) si proprietatile ei a ∧ a = 0 si a ∧ b = b ∧ a. Vom face suma xor a numerelor a[i] ∧ i (1 <= i <= n):
S = a[ 1 ] ∧ 1 ∧ a[ 2 ] ∧ 2 ∧ ... ∧ a[ n - 1 ] ∧ n - 1 ∧ n
Astfel fiecare numar care apare in sir va fi in suma de doua ori si va fi anulat, iar rezultatul final va fi indicele numarului lipsa. Solutia are compexitatea O(n) ca timp si O(1) ca spatiu.
Problema 2 ( interviu Microsoft )
Se da un sir de n+1 numere de la 1 la n in care unul se repeta, iar restul sunt distincte. Sa se dea un algoritm cat mai eficient care sa determine numarul ce se repeta.
Rezolvare
Evident, abordarile de la problema anterioara se aplica si aici.
Problema 3 ( lot 1999, interviu Microsoft )
Se da o lista inlantuita prin primul ei element. Se cere un algoritm cat mai eficient care sa determine daca lista are sau nu ciclu.
Rezolvare
Fie n numarul total de elemente ale listei. O solutie triviala in O(n) timp si O(n) memorie ar fi sa parcurgem lista si sa adaugam pe rand elementele unui tabel de dispersie (cand apare de doua ori acelasi element rezulta ca am gasit un ciclu). O metoda folosita de unii concurenti este parcurgerea listei pe o perioada de timp determinata (timpul de executie fixat), fiind sanse mari ca un ciclu sa nu existe daca nu s-a gasit nici unul pana la momentul incheierii executiei.
Exista un algoritm mai elegant, care ruleaza tot in timp liniar. El se numeste Algoritmul lui Floyd de detectie a ciclului intr-o lista. O aplicatie importanta este Algoritmul Pollard ρ, folosit pentru factorizarea intregilor cu multe cifre. Se folosesc doi pointeri a si b, unde a se misca de doua ori mai repede decat b in lista (denumit si Algoritmul iepurelui si testoasei). Reprezentarea grafica seamana cu litera greceasca ρ. Notam lungimea lantului cu λ si lungimea ciclului cu μ.
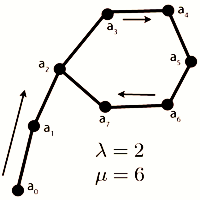
//cap - pointer spre capatul listei
a = b = cap;
do{
b = b -> next;
a = a -> next -> next;
}while(a != b);Cand a si b sunt amandoi in ciclu, este evident ca la un moment dat a = b. In exemplul desenat, dupa sase iteratii cei doi pointeri vor indica acelasi element. Pentru determinarea lungimii ciclului se mai poate face o parcurgere in care doar un pointer se misca. Acum dupa ce stim lungimea μ a ciclului, putem afla si lungimea λ a lantului astfel: luam un pointer la inceputul listei si al doilea care a facut deja μ pasi in lista (amandoi pointerii au aceeasi viteza). Dupa λ pasi ei vor fi egali. Astfel am obtinut o rezolvare liniara.
Problema 4 ( IBM Research: Ponder This )
Un sir de lungime n contine numere intregi din multimea {1, 2, ..., n-1}. Folosind Principiul lui Dirichlet deducem ca cel putin un element se repeta. Gasiti un algoritm liniar care afiseaza o valoare ce se repeta, folosind memorie suplimentara constanta si nemodificand la nici un pas vreun element din sir.
Rezolvare
Aici nu merge solutia cu suma xor de la problemele 1 si 2 pentru ca numerele pot fi repetate oricum si nu putem folosi relatiile obtinute pentru a determina un numar care se repeta. Daca toate elementele din sir ar fi distincte, atunci sirul ar avea structura unei permutari. Cum ele nu sunt neaparat distincte ne vine ideea de a vedea care este diferenta intre un asemenea sir si o permutare, pentru a folosi idei care apar la permutari (ciclurile acestora). Fiecare element din sirul nostru indica inspre altul, deci il putem considera un graf orientat in care arcele sunt (i, a[i]). De exemplu putem face urmatoarea reprezentare pentru sirul 3, 2, 1, 3, 4:
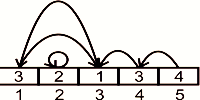
Din fiecare nod iese cate un arc si cum sunt un numar finit de noduri rezulta ca din orice nod pornim ajungem intr-un ciclu. In momentul in care intram in ciclu, acel numar se va repeta, deci vrem ca primul nod sa nu apartina nici unui ciclu. Un astfel de nod e nodul n, pentru ca nici un element a[i] nu va fi egal cu n. Deci, daca pornim de la nodul n suntem in afara oricarui ciclu si putem sa mergem pe drumul pe care il indica pentru a ajunge eventual intr-un ciclu. Am vazut in problema anterioara cum determinam lungimea lantului pentru o lista ce contine un ciclu. Putem determina astfel elementul de la intrarea in ciclu in complexitate O(n) si problema noastra este rezolvata.
Problema 5
Se da un sir de N intregi ce contine numere intre 1 si N. Sa se determine cat mai eficient daca acest numar este o permutare, fara a distruge sirul.
Rezolvare
Pentru ca valorile sirului sunt intregi, iar valorile elementelor unei permutari sunt pozitive, rezulta ca putem folosi bitul de semn al fiecarui numar pentru ca acesta ramane liber. Verificam mai intai daca exista vreun element negativ in sir. Apoi, daca nu exista, vom marca elementele parcurse din ciclurile permutarii astfel a[i] = -a[i]. Daca un element este marcat de doua ori sau am gasit initial un numar negativ, atunci cele N numere nu reprezinta o permutare. Pentru a reface sirul initial, vom schimba toate elementele ce au semn negativ din sir cu valorile lor in modul. Astfel am obtinut o rezolvare liniara ce foloseste spatiu suplimentar O(1).
Problema 6 ( interviu Microsoft )
Se dau n numere de la 1 la n. Unul din ele unul apare de doua ori in sir, iar restul sunt distincte. Evident ca un numar nu va aparea niciodata. Sa se dea un algoritm cat mai eficient care sa determine numarul lipsa si numarul ce apare de doua ori.
Rezolvare
Notam cu a numarul lipsa si cu b numarul ce apare de doua ori. Majoritatea celor care stiu sa rezolve problema 1 prin cele doua solutii optime (suma numerelor si suma xor) incearca sa rezolve aceasta problema determinand doua relatii diferite asupra lui a si b, din care apoi incearca sa obtina valorile cerute. Scazand din n(n + 1)/2 suma numerelor din fisier obtinem valoarea pentru a - b, iar facand suma xor a numerelor din fisier si a numerelor de la 1 la n obtinem valoarea pentru a ∧ b. In acest moment putem considera ca problema este rezolvata, dar la o analiza mai atenta se poate observa ca numerele care verifica relatiile respective nu sunt unice. De exemplu pentru a = 10 si b = 9 obtinem valorile a - b = 1 si a ∧ b = 3. Aceleasi valori le obtinem si pentru a = 6 si b = 5. Se observa de aici ca cele doua relatii nu pot fi folosite pentru a rezolva problema.
Stim care este valoarea diferentei D1 = a - b, dar mai avem nevoie de o relatie pentru a determina numerele a si b. Vom incerca in continuare sa folosim operatia de inmultire pentru a obtine cea de-a doua relatie. Vom avea: a/b = n! / (a[ 1 ] * a[ 2 ] * ... * a[ n ]). Aceasta relatie nu poate fi calculata in O(n) pentru ca numarul de cifre al lui n! nu este constant. Pentru a evita lucrul cu numere mari am putea sa logaritmam intreaga relatie, obtinand lg a - lg b = lg 1 + lg 2 + ... + lg n - lg a[ 1 ] - lg a[ 2 ] - ... - lg a[ n ]. Aceasta rezolvare ar fi buna daca ar fi posibila realizarea unor calcule perfecte cu numere reale. Din pacate acest lucru nu este posibil si rezolvarea are mari probleme cu precizia.
O a doua relatie o putem obtine ca diferenta intre suma patratelor numerelor de la 1 la n si suma patratelor numerelor din fisier. Obtinem astfel D2 = a2 - b2. Din aceste doua relatii putem usor afla ca a = (D1 + D2/D1)/2 si b = (D2/D1 - D1)/2. Aceasta rezolvare are complexitatea O(n) ca timp si O(1) ca spatiu.
Problema 7
Se dau n - k numere distincte de la 1 la n. Sa se dea un algoritm cat mai eficient care sa determine numerele lipsa.
Rezolvare
Fie a, b, c, ... numerele ce lipsesc. Am putea extinde ideea din problema anterioara pentru a obtine in O(n*k) sumele S1 = a + b + c + ..., S2 = a2 + b2 + c2 + ..., ..., Sk = ak + bk + ck + ... si sa obtinem valorile elementelor a, b, c, ..., dar in general daca valoarea lui k este variabila, atunci putem gasi solutia ce satisface toate cele k relatii in timp exponential. O metoda este de a transforma relatiile intr-un polinom de radacini a, b, c, .... Pentru a gasi P(x) = a0Xk + a1Xk-1 + ... + ak putem folosi relatiile lui Viete1
s1 = a + b + c + d + ...
s2 = ab + ac + ad + bc + bd + cd + ...
s3 = abc + acd + bcd + ...
s4 = abcd + ...
...
si = (-1)i an-i/an
Aceste sume sk sunt numite polinoame simetrice si sunt strans legate de sumele de puteri k Sk prin relatiile Newton Girard2. Astfel avem un algoritm ce determina polinomul in O(nk) si spatiu O(k) (daca se ignora faptul ca numerele ar putea depasi intervalul numerelor reprezentabile pe un intreg), dar determinarea solutiei finale se poate face in O(1) doar pentru ecuatii de gradul doi sau trei, pentru care stim formule de calcul. Pentru ecuatii de grad mai mare nu exista formule generale si trebuie aplicate metode care aproximeaza solutiile. O astfel de metoda ar fi sa derivam polinomul, sa gasim solutiile pentru P'(x) = 0, iar apoi sa folosim cate o cautare binara pentru a gasi solutiile P(x) = 0.
De exemplu pentru trei numere lipsa a, b, c este usor sa determinam S1 = a + b + c, S2 = a2 + b2 + c2, S3 = a3 + b3 + c3. S12 = a2 + b2 + c2 + 2ab + 2bc + 2ac = S2 + 2s2, S13 = a3 + b3 + c3 + 3a2b + 3a2c + 3b2a + 3b2a + 3c2a + 3c2b + 6abc = S3 + 3(a2b + b2a + abc) + 3(a2c + c2a + abc) + 3(b2c + c2b + abc) - 3abc = S3 + 3ab*s1 + 3ac*s1 + 3bc*s1 - s3 = S3 + 3s2*s1 - s3. Din aceste relatii putem sa obtinem usor s1, s2, s3 si apoi putem aplica formulele lui Cardano de rezolvare a ecuatiei de gradul trei pe ecuatia x3 - s1 x2 + s2 x - s3 = 0.
Problema 8
Intr-o structura de date avem n - 1 numere intregi (pentru simplitate n = 2b - 1, cu numere distincte de la 0 la n). Asupra elementelor din structura de date putem face urmatoarea operatie <code>getBit(i, j)</code>, care returneaza al j-lea bit din reprezentarea binara a numarului a[ i ]. Astfel daca a[ 4 ] = 11, atunci <code>getBit(4, 3)</code> returneaza 0 pentru ca 11 se scrie in baza 2 ca 1011. Sa se dea o solutie eficienta care gaseste numarul lipsa.
Rezolvare
Acum vom folosi din nou un algoritm bazat pe Divide et Impera. La primul pas impartim multimea in doua submultimi - cea a numerelor pare si cea a numerelor impare, si vedem in care din ele se gaseste numarul nostru lipsa (am aflat astfel ultimul bit al rezultatului). Acum putem aplica recursiv procedura aceasta pe numerele din o lista cu jumatate din lungimea listei initiale impartite la doi (ignoram ultimul bit al numerelor). Aceasta solutie are complexitate O(n) pentru ca dupa fiecare pas executat in timp liniar, dim
