Superpoligon
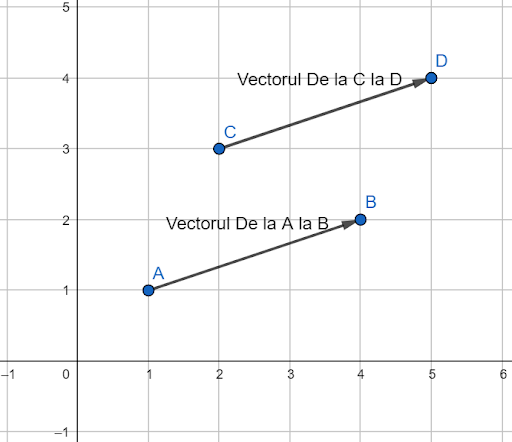
Pentru a simplifica solutia, o sa introducem notinunea de vector de translatie. Vectorul de translatie este o pereche { a, b }, si reprezinta o deplasare a unui punct / poligon / dreapta etc in plan. In figura de mai sus vectorul AB este egal cu vectorul CD.
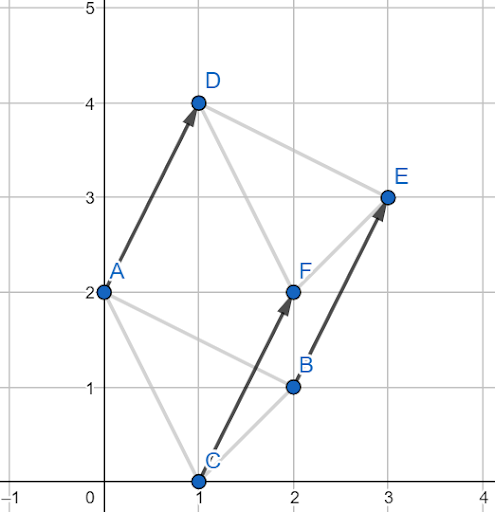
In figura alaturata, se poate vedea triunghiul ABC care este confundabil cu triunghiul DEF. Pentru a verifica confundabilitatea, putem sa verificam ca vectorul AB = DE, BC = EF, CA = FD.
Prelucram egalitatea AB = DE <=> AD + DE + EB = DE <=> AD + EB = 0 <=> AD = BE.
Analog, trebuie ca AD = CF.
Din ecuatiile de mai sus reiese ca AD = CF = BE.
Doua poligoane sunt deci confundabile daca si numai daca varfurile unuia pot fi obtinute din varfurile celuilat carora adaugam acelasi vector de translatie.
Pentru fiecare doua varfuri nu neaparat distincte, calculam vectorul de translatie (perechea { dx, dy }), pe care le punem intr-o structura de hash, cum ar fi std::map, vector static + sortare, tabla de hash etc, care sa poata tine minte frecventa unui vector (de cate ori a fost adaugat – cate perechi distincte au acel vector de translatie).
Acum, doua poligoane sunt confundabile daca si numai daca toate perechiile de varfuri corespunzatoare au acelasi vector de translatie. Putem deci fixa vectorul si stim cate perechi convenabile de varfuri avem.
Pentru a gasi numarul de poligoane confundabile, iteram prin toti vectorii de translatie posibili. Sa presupunem ca ne-am fixat un vector de translatie { x, y } care apare de w ori. Faptul ca apare de w ori garanteaza ca exista w puncte din care se poate forma un poligon, si ca perechiile lor formeaza un poligon confundabil.
Un poligon fiind un vector circular (rotirea nu conteaza), numarul de moduri de-a alege un poligon de a varfuri dintr-un set de b puncte este (aranjamente de b luate cate a) / a.
Numarul de perechi de varfuri fiind 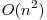 , complexitatea algoritmului de mai sus, presupunand aranjamentele si impartirea
, complexitatea algoritmului de mai sus, presupunand aranjamentele si impartirea 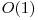 , este
, este 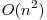 sau
sau 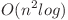 , in functie de metoda de hash folosita.
, in functie de metoda de hash folosita.
Notam cu A(x, y) aranjamente de x luate cate y si cu C(a, b) combinari de a luate cate b.
A(x, y) / y = (x! / (x - y)!) / y = x! / ((x - y)! * y!) * (y - 1)! = C(x, y) * (y - 1)!.
Combinarile pot fi calculate in 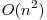 si factorialele in
si factorialele in 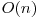 , cu
, cu 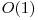 pe intrebare.
pe intrebare.
Complexitatea finala este deci 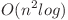 sau
sau 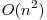 .
.
Observatii
- Este posibil ca solutii neoptimizate dar cu complexitatea buna sa ia TLE. De exemplu solutiile cu map fara optimizari suplimentare iau TLE. Alternativa cea mai simpla este sa punem toti vectorii intr-un vector static si sa il sortam. Desi are aceeasi complexitate teoretica este mult mai eficient.
- Subtaskurile cu modulul neprim se bazeaza pe calculul de mai sus care nu necesita impartiri.
