Revizia anterioară Revizia următoare
Solutii runda 2
Suntem bucurosti ca runda 2 a concursului Autumn Warmup 2007 s-a incheiat cu bine. Acest articol va va prezenta solutiile celor 4 probleme propuse spre rezolvare, precum si cateva aprecieri in legatura cu desfasurarea probei.
Spre deosebire de prima runda, am incercat sa variem cat mai mult dificultatea problemelor, pentru a le permite tuturor sa se pregateasca. Au fost 2 probleme usoare (Trompeta si MMsir), una de dificultate medie (Curcubeu), iar ultima a fost "rupere" (Rompetrol), nivelul de dificultate al acestea fiind crescut chiar si pentru o competitie gen IOI. Il felicitam pe veteranul Codrut Grosu, care a fost singurul concurent ce a obtinut maxim la aceasta problema.
Aruncandu-ne privirea peste clasamentul rundei, observam in frunte membri vechi ai comunitatii, cu rezultate anul acesta la olimpiadele internationale. Runda a fost castigata de Bogdan Tatataroiu care a reusit sa se impuna cu 3 probleme rezolvate aproape corect si cu un brute-force la Rompetrol. Pe locul 2 s-a clasat Cosmin Gheorghe, iar pe 3 Victor Rusu. Ii felicitam atat pe ei, cat si pe ceilalti participanti.
Spre deosebire de prima runda, remarcam o oarecare omogenitate a punctajelor si speram ca v-au placut problemele. Daca aveti sugestii despre cum am putea sa imbunatatim concursul, le asteptam pe forum. In continuare va prezentam solutiile problemelor din concurs.
Curcubeu
Vom considera colorarile incepand cu ultima. Parcurgem intervalul asociat ei si de fiecare data cand gasim o casuta necolorata ii asociem valoarea C<sub>$i$</sub>. Aceasta solutie are complexitatea O(N2) si ar fi obtinut 20 de puncte. Pentru punctaj maxim este nevoie de un rafinament. Analizand solutia anterioara, observam ca vom parcuge de foarte multe ori castue deja colorate, lucru inutil si consumator de timp. Pentru fiecare pozitie i vom mentine o valoare Next[i], semnficand faptul ca intervalul [i, Next[i]-1] contine doar casute colorate (initial Next[i] = i). Astfel, la colorarile urmatoare, vom putea "sari" peste secvente intregi de pozitii anterior colorate. Pentru a implementa eficient aceasta solutie, putem folosi una din cele doua euristici ale structurilor pentru multumi disjuncte, cea a comprimarii drumului. Puteti citi mai multe despre structuri pentru multimi disjuncte in Cormen sau aici. Complexitatea finala este O(N log* N). De mentionat faptul ca se pot obtine 50 de puncte implementand solutii de complexitate O(N log N) folosind arbori de intervale sau un maxheap.
Trompeta
Problema se rezolva cu metoda greedy. Se formeaza treptat rezultatul cu ajutorul unei stive: daca cifra curenta este mai buna decat cea din varful stivei si numarul de cifre din stiva + numarul de cifre ramase ≥ M, atunci elementul din varful stivei este eliminat. Acest algoritm are complexitate O(N).
MMsir
Vom rezolva problema in o(n) folosind 2 contori, st si dr, si 2 vectori, h[i]=1 daca si numai daca a[i-1] < a[i] > a[i+1] sau a[i-1] > a[i] < a[i+1], si schimb[i] care va fi egal cu cel mai mic j cu propietatea ca h[j]=1 si j>i. De aici vom incepe sa construim solutia astfel: initial dr va fi egal cu cel mai mic i cu propietatea ca secventa 1 i isi schimba monotonia de k ori, iar st va fi egal cu 1. Incepem sa incrementam dr cu cate o unitate si de fiecare data adunam la solutie schimb[st] - st. Atunci cand h[dr-1] = 1, st ia valoarea schimb[st].
Pentru o rezolvare brute cu complexitate o(n^2) se acordau 30 de puncte.
Rompetrol
Vom calcula costurile cmin[ i ][ j ][ 0 ] si cmin[ i ][ j ][ 1 ], avand semnificatiile:
cmin[ i ][ j ][ 0 ]= costul minim pentru a amplasa in total i depozite in benzinariile [1..j], iar al i-lea depozit se afla localizat chiar in benzinaria jcmin[ i ][ j ][ 1 ]= costul minim pentru a amplasa in total i depozite in benzinariile [1..j, iar al i-lea depozit nu este neaparat amplasat in benzinaria j
Relatiile de recurenta sunt urmatoarele:
cmin[ i ][ j ][ 0 ] =
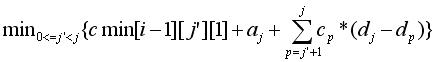
cmin[ i ][ j ][ 1 ] =
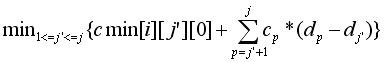
Valorile initiale sunt:
- cmin[ 0 ][ 0 ][ 0 ] = cmin[ 0 ][ 0 ][ 1 ] = 0
- cmin[ 0 ][ i ][ 0 ] = cmin[ 0 ][ i ][ 1 ] = infinit, pentru i > 0
Observand ca in relatiile de recurenta toate valorile cmin[i][a][b] depind doar de valori de tipul cmin[i-1][a1][b1] si cmin[i][a2][b2], putem retine doar ultimele 2 linii ale matricii cmin, pentru a nu ocupa prea multa memorie.
Prima solutie pleaca de la implementarea directa a relatiilor de recurenta si are complexitatea O(N2*K), in conditiile in care putem calcula in O(1) sumele dupa p ce apar in relatiile de recurenta. Acest lucru se poate realiza usor, calculand in timp O(N) urmatoarii vectori:
- csum[i] = suma cantitatilor de combusitibil din benzinariile [1..i] ; csum[i] = csum[i-1]+c[i]
- cright[i] = suma costurilor de a transporta cantitatile necesare de combustibil de la benzinaria N la fiecare din benzinariile [i..N] ; cright[i] = cright[i+1] + c[i] * (d[N] - d[i])
- cleft[i] = suma costurilor de a transporta cantitatea dorita de combustibil de la benzinaria N la benzinariile [i..N] ; cleft[i] = cleft[i-1] + c[i] * (d[i] - d[ 1 ])
Cu acesti vectori, 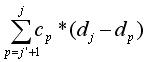 se scrie ca fiind egala cu cright[j1+1] - cright[j+1] - (csum[j] - csum[j1]) * (d[N] - d[j]). In mod similar,
se scrie ca fiind egala cu cright[j1+1] - cright[j+1] - (csum[j] - csum[j1]) * (d[N] - d[j]). In mod similar, 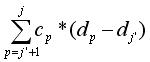 se scrie ca fiind egala cu cleft[j] - cleft[j1] - (csum[j] - csum[j1])*(d[j1] - d[ 1 ]).
se scrie ca fiind egala cu cleft[j] - cleft[j1] - (csum[j] - csum[j1])*(d[j1] - d[ 1 ]).
Solutia optima are, insa, complexitatea O(N*K) si se bazeaza pe urmatoarele concepte: pentru fiecare i de la 1 la K si fiecare pozitie j de la 1 la N vom defini doua functii fi,j si gi,j, pe care le vom folosi in calculul valorilor cmin[ i ][ j ][ 0 ] si cmin[ i ][ j ][ 1 ].
Calculul valorilor cmin[ i ][ j ][ 0 ]
Pentru fiecare pozitie j, vom defini functia fi,j:[d[j],d[N]] -> int. O valoare a acestei functii intr-un punct d[p], corespunzator benzinariei p, fi,j(d[p]), reprezinta costul minim pentru a amplasa i depozite in benzinariile 1,2,..,p, in conditiile in care al i-lea depozit este in benzinaria p, iar benzinariile j, j+1, .., p sunt alimentate cu combustibil de la depozitul din benzinaria p. Cu aceste definitii, valoarea lui cmin[ i ][ j ][ 0 ] este minimul dintre valorile functiilor fi,j1, in punctul d[j], cu 0<=j1<j, la care se adauga valoarea a[j]. Problema importanta este cum aflam minimul dintre aceste functii, fara a calcula valoarea fiecarei functii in punctul d[j] (care ar conduce la o complexitate O(N2*K)).
Formula unei functii fi,j(d[p]) este: cmin[ i-1 ][ j-1 ][ 1 ] + 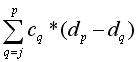 . Diferenta dintre 2 valori consecutive ale functiei, dfi,j(d[p+1]) = fi,j(d[p+1]) - fi,j(d[p]), este egala cu (c[j]+c[j+1] + .. + c[p]) * (d[p+1] - d[p]). Asadar, de la un pas la altul, functiile fi,j care au un j mai mic cresc mai mult decat cele care corespund unei pozitii j mai mari (altfel spus, functiile care au aparut mai recent cresc mai incet decat functiile care au aparut de mai mult timp) : dfi,j(d[p+1]) < dfi,j1(d[p+1]), daca j1 < j. De aici tragem urmatoarele concluzii:
. Diferenta dintre 2 valori consecutive ale functiei, dfi,j(d[p+1]) = fi,j(d[p+1]) - fi,j(d[p]), este egala cu (c[j]+c[j+1] + .. + c[p]) * (d[p+1] - d[p]). Asadar, de la un pas la altul, functiile fi,j care au un j mai mic cresc mai mult decat cele care corespund unei pozitii j mai mari (altfel spus, functiile care au aparut mai recent cresc mai incet decat functiile care au aparut de mai mult timp) : dfi,j(d[p+1]) < dfi,j1(d[p+1]), daca j1 < j. De aici tragem urmatoarele concluzii:
- daca valoarea unei functii fi,j(d[p+1]) este mai mare decat valoarea unei functii fi,j1(d[p+1]), cu j1>j, atunci functia fi,j nu va mai avea niciodata valoarea minima dintre toate functiile la nici unul din pasii ulteriori.
- daca valoarea unei functii fi,j(d[p+1]) este mai mica decat valoarea unei functii fi,j1(d[p+1]), cu j1>j, atunci functia fi,j va fi 'depasita' de functia fi,j1 intr-un punct xj,j1 ; maximul dupa j dinte valorile xj,j1 reprezinta punctul minim posibil la care functia fi,j1 va avea valoarea minima dintre toate functiile dinaintea ei.
Cu aceste observatii, putem folosi un deque in cadrul algoritmului nostru, care contine functiile 'aparute' pana la fiecare pas p. Functiile sunt sortate dupa valoarea lor la pasul p, precum si dupa momentul la care urmeaza sa devina functii cu valoare minima. La fiecare pas p se introduce in deque o functie noua, functia fi,p. Aceasta va elimina toate functiile care au la pasul p o valoare mai mare decat a ei, precum si acele functii pe care le-ar depasi intr-un punct x mai mic decat momentul minim posibil la care acestea ar putea deveni functii cu valoare minima (pentru ca, astfel, acestea nu vor mai deveni niciodata functii cu valoare minima). De asemenea, la fiecare pas p se elimina din partea din fata a deque-ului functiile pentru care functia de dupa ea are punctul in care devine minima mai mic sau egal cu d[p].
Pentru a calcula punctul xj,j1 in care o functie fi,j1 depaseste o functie fi,j (j<j1), trebuie sa calculam urmatoarele valori. Sa presupunem ca ne aflam la pasul p=j1. Vom calcula dC = fi,j1(d[j1]) - fi,j(d[j1]). Vom observa acum ca functiile fi,j au fost definite pe un interval de distante, deoarece, intre doua distante corespunzatoare a doua benzinarii consecutive, ele se comporta ca niste drepte. La pasul p=j1, dreapta corespunzatoare functiei fi,j are o panta egala cu dP=(c[j] + c[j+1] + .. + c[j1-1]), iar dreapta corespunzatoare functiei fi,j1 are panta 0. In fiecare punct mai mare decat punctul d[j1], diferenta dintre pantele dreptelor corespunzatoare celor 2 functii in punctul respectiv va ramane constanta si egala cu dP. Se observa
usor ca acest lucru este adevarat, pentru ca pantele dreptelor asociate cresc cu aceeasi valoare in fiecare punct in care se afla localizata o benzinarie. Prin urmare, punctul x in care functia fi,j1 depaseste functia fi,j este x=d[j1] + dC/dP.
Calculul valorilor cmin[ i ][ j ][ 1 ]
Calculul valorilor cmin[ i ][ j ][ 1 ] se realizeaza similar cu calculul valorilor cmin[ i ][ j ][ 0 ]. Se vor defini niste functii gi,j:[csum[j], csum[N]], ale caror valori gi,j(csum[p]) vor reprezenta costul minim pentru a amplasa i depozite in benzinariile [1..p], in conditiile in care al i-lea depozit este amplasat in benzinaria j. Aceste functii sunt definite pe sumele partiale ale cantitatilor de combustibil pentru a putea folosi un rationament asemanator celui prezentat mai sus si a privi fiecare functie ca o dreapta in intervalul dintre sumele partiale corespunzatoare a doua benzinarii consecutive. Panta unei functii gi,j intr-un punct csum[j1] (j1>j) va fi, conform acestor definitii, d[j1]-d[j].
