Solutii Adolescent Grigore Moisil 2016
Arcas
O prima observatie este aceea ca daca mutam tintele de la coordonata x cu x pozitii mai jos (adica tintele de forma x y1 y2 devin x y1-x y2-x) si punctul de tragere de la coordonata x il mutam deasemena cu x pozitii mai jos (adica tragerea de forma x y r devine x y-x r) atunci si traiectoria sagetii se modifica, aceasta devenind orizontala (adica sageata va traversa punctele de coordonate ( x, y-x ), ( x+1, y-x ), ( x+2, y-x ),…, ( x+r, y-x ) ).
Sageata de tipul x’ y’ r nimereste tinta de tipul x y1 y2 <=> exista un r’, 0 <= r’ <= r astfel incat punctul ( x’+ r’, y’+ r’ ) se afla pe tinta <=>
1) x’ + r ’= x
2) y1 <= y’ + r’ <= y2
<=> r’ = x - x’ => y1 <= y’ + x – x’ <= y2 <=> y1 – x <= y’ – x’ <= y2 - x
De unde rezulta ca intersectia este echivalenta cu existenta unui r’ cu 0 <= r’ <= r astfel incat:
1) x’ + r’ = x
2) y1 – x <= y’ – x’ <= y2 – x
Ceea ce este echivalent cu sageata sa nimereasca tinta dupa transformarea de mai sus.
Asadar, problema s-a redus la cate segmente verticale intersecteaza un segment orizontal. Numarul de segmente verticale care sunt intersectate de segmenul orizontal de la ( a1, b) la ( a2, b ) sunt numarul de segmente verticale de la ( x, y1 ) la ( x, y2 ) cu a1 <= x <= a2 si y1<= b <= y2, care este de fapt numarul de segmente verticale cu x <= a2 si y1 <= b <= y2 minus numarul de segmente verticale cu x <= a1 – 1 si y1 <= b <= y2. Acest lucru se poate face online cu un arbore de intervale persistent sau offline cu AIB sau Arbint.
Solutia online: pentru fiecare tinta de forma x y1 y2 se face un update la timpul x si la pozitia y1 din arbint cu +1 si un update la timpul x si la pozitia y2 + 1 din arbint cu -1. Iar raspunsul pentru o sageata de tipul a b r este raspunsul query-ului de la timpul a + r si de la pozitia b din arbint (adica care este suma elementelor de la 1 la b) minus query-ul de la timpul a - 1 si la pozitia b din arbint (adica, deasemenea, care este suma elementelor de la 1 la b).
Solutia offline este mult mai simpla si mai accesibila: o sa avem evenimente de forma x y s care semnifica adaugarea la timpul x pe pozitia y valorii s si evenimente de tipul x y tip poz cu semnificatia ca la raspunsul pentru tragearea poz se adauga/scade (daca tip = 0 se adauga, daca tip = 1 se scade) suma elementelor de la 1 la y de la timpul x. Pentru fiecare tinta de forma x y1 y2 se adauga in lista de evenimente ( x y1 1 ) si ( x y2+1 -1 ) si pentru fiecare tragere i de forma a b r se adauga in lista de evenimente ( a+r b 0 i ) si ( a-1 b 1 i ). Se sorteaza aceste evenimente dupa x si se simuleaza updateurile/query-urile pe un AIB sau Arbint (de notat faptul ca in urma sortarii, primul tip de eveniment descris mai sus de la timpul x trebuie sa apara inaintea celui de-al doilea tip de eveniment descris de la timpul x).
Atentie ca pentru ambele solutii e necasara o normalizare sau adunarea unei constante la toate valoriile de pe OY.
Complexitatea in ambele cazuri este O ( ( N + M ) * log ( N + M ) ).
PS: Colegii mei au zis sa nu fim jegosi si sa nu dam sa intre doar solutia online si sa dam limita coordonatelor 105 ca sa se poata face acea adunare la toate valoriile de pe OY (destul de draguta #comisia zic eu:) ).
Centrale Nucleare
Putem cauta binar distanta D la care nu se pot alege 2 puncte la distanta <= D. Astfel solutia problemei este D + 1.
Fie D distanta curenta din cautarea binara. Daca aceasta distanta este buna atunci trebuie cautata una mai mica, altfel una mai mare. Deci problema s-a redus la determinarea posibilitatii alegerii unor puncte care sa satisfaca cele M restricitii din enunt si distanta intre oricare 2 sa fie > D. Acest lucru se poate face cu 2SAT. Daca notam valoarea variabilei x cu selectarea sau nu a centralei x, atunci cele M restrictii devin propozitii de forma ( x | y ) iar pentru fiecare pereche ( x , y ) de centrale cu distanta <= D impunem propozitia ( !x | !y ), unde cu | am notat operatorul sau, si cu !x am notat negarea valorii lui x. Complexitatea 2SAT-ului este O ( N + M ), unde N = numarul literarilor si M = numarul propozitiilor. In problema noastra numarul de literari este N si numarul de propozitii este M + N2. Plus cautarea binara avem o complexitate finala O ( log ( distanta maxima ) * ( M + N2 ) ), ceea ce este un pic cam mult. Totusi trebuie sa ne gandim de ce autorul problemei a dat distanta Manhattan pentru ca solutia descrisa mai sus merge si pentru distanta normal, cea Euclidiana. Ceea ce ne deranjaza in complexitatea de mai sus este acel N2, deci trebuie sa exploram mai mult care sunt de fapt punctele care nu pot fi alese atat timp cat e ales si punctul i, aceste puncte fiind de fapt acelea care sunt la distanta Manhattan <= D de punctual i, adica acele puncte care se afla in rombul cu centrul in punctul i si de diagonala 2*D. Dar acest romb se transforma intr-un patrat de latura 2*D si centru in punctul i daca rotim planul cu 45 de grade (Hmm un patrat, o chestie destul de simetrica si mai simpla din unele puncte de vedere, pai poate de-asta a dat autorul distanta Manhattan, hai sa continuam cu ideea aceasta). Deci punctele care nu pot fi luate atat timp cat este luat punctul i sunt acele puncte care se afla in patratul cu centrul in punctul i de latura 2*D, deci avem propozitiile ( !i | !y ), pentru toate punctele y care apartin patratului cu centrul in i si de latura 2*D. Sa ne gandim un pic si la cum se rezolva 2SAT-ul: o sa ne construim un graf pe care o sa bagam tare conexe, pentru fiecare propozitie de forma ( x | y ), de fapt introducem in graf muchiile !x -> y si !y -> x deci pentru propozitia de mai sus avem muchia i -> !y (este de ajuns doar aceasta muchie pentru ca muchia y -> !i va fi adaugata de propozitia ( !y | !i ) ). Deci avem muchiile i -> !y pentru oricare i de la 1 la N si pentru oricare y care se afla in patratul cu centrul in i si de latura 2*D. Ca sa rezolvam 2SAT-ul usor ne construim graful si aplicam algoritmul lui Kosaraju si daca cumva si x si !x se afla in aceeasi componenta tare conexa => nesatisfiabilitate. Acum un lucru care trebuie retinut, si anume acela ca in informatica nu trebuie sa invatam algoritmi pe de rost, nici macar numele acestora, cum ar fi ca acesta se cheama Kosaraju (singurul folos in a stii acest lucru este doar ca sa te intelegi mai bine cu cineva caruia ii explici o solutie), trebuie sa ne gandim logic si sa vedem ce face acesta. El consta intr-un DFS in care marcam nodurile ca si vazute si le adaugam intr-o coada si apoi inca un DFS, numai ca pe graful transpus, pornind din noduri in ordinea inversa adaugarii in coada (aceasta fiind de fapt si sortarea topologica) in care demarcam nodurile. Aaa, deci niste DFS-uri, hmm, pai la fiecare pas in DFS mie imi trebuie un vecin al nodului curent care nu a fost vizitat pana acum, hmm, deci multe muchii nu o sa le folosesc. Aaaa, pai poate asta e, ia sa vedem cum putem sa gasim un vecin care nu a fost vizitat de-al nodului nod in timp rezonabil. Pai vecinul vec al nodului nod este, de fapt, un punct care se afla in patratul cu centrul in punctul nod si de latura 2*D. Deci am redus problema la aflarea unui punct din interorul unui patrat. Acest lucru se poate face folosind set-uri si Arbint: normalizam toate punctele dupa x si construim un arbint care are in fiecare nod cate un set in care introducem toate punctele care corespund intervalului curent, Acest set il tinem sortat dupa y. De remarcat ca numarul total de elemente inserate in set-uri este N * log ( N ). Iar query-ul se poate rezolva selectand din intervalul ( xi – D; xi + D ) cel mai aproape punct ca distanta pe OY de ( xi, yi ) si sa vedem daca acesta are distanta aceasta <= D, ceea ce se poate face printr-un query in arbint unde la fiecare pas cand intervalul curent este inclus in cel de query ne folosim de set sa determinam cel mai aproape punct pe OY. Si de fiecare data cand gasim un vecin facem un update in arbint si eliminam punctul din toate set-urile care il contin. Acest arbint are complexitate O ( N * log ( N ) 2 ) pentru constructie si O ( log ( N ) 2 ) pentru query respectiv update, dar cum sunt maxim N noduri carora le vrem vecin complexitatea devine O ( N * log ( N ) ^ 2 ).
Iar pentru propozitiile corespunzatoare celor M restrictii putem sa le tinem graful fara nicio problema. Deci complexitate O ( M ).
Deci complexitatea finala este O ( log ( distanta maxima ) * ( M + N * log ( N ) ^ 2 ) ).
Determinarea acelui vecin se mai poate face si cu semnul lui Batog care este tot la fel numai ca se imparte in bucati de radical pe care se tine cate un set. Complexitate O ( log ( distanta maxima ) * ( M + N * log ( N ) * sqrt ( N ) ) ).
Datorita diferentei foarte mare intre numarul de set-uri intre cele 2 solutii si diferentei destul de mica intre log ( N ) si sqrt ( N ) pentru limita lui N, surprinzator (sau poate ca nu), a doua solutie se misca mult mai bine.
PS: La rotirea unui plan cu 45 de grade acel √2 se da factor comun peste tot, deci putem rotii planul usor transformand punctul ( x, y ) in punctul de coordonate ( x - y, x + y ).
HardTask
Prima observatie este ca numarul total de lca-uri dintre elementele multimii sunt maxim cardinalul acesteia ( de fiecare data selectam 2 noduri care produc un lca care nu mai are niciun nod in subarbore, inafara de cele 2, si il adaugam pe acesta in multime in locul celor 2 => cardinalul multimii scade cu 1, deci acest procedeu se repeta de maxim nr ori ). Aceste lca-uri plus nodurile din multime sunt, de fapt, singurele noduri de interes pentru rezolvarea query-ului. O sa ne construim arborele numai cu aceste noduri, adica comprimam arborele initial la aceste noduri. Deci am redus problema la aceeasi numai ca pe un arbore cu 2*nr noduri. Aceasta se poate face in complexitate O ( nr * log ( nr ) ^ 2 ) cu smenul ca daca in dfs, pe langa apelarea dfs-ului pentru fiecare fiu, mai parcurgem inca o data toate nodurile din subarborele nodului curent inafara de cele din subarborele fiului cel mai greu, complexitatea finala este O ( nr * log ( nr ) ). Asadar pentru fiecare nod o sa ne tinem o lista, de fapt un map, in care o sa introducem toate nodurile din subarbore cu costul pana la radacina modulo K. Aceasta lista se preia de la fiul cel mai greu si celelalte liste ale celorlalti fii se parcurg si cu ajotorul map-ului putem determina cate perechi de noduri care au drumul divizibil cu K si au lca-ul in nodul curent exista.
In continuare sa vedem cum putem determina aceste lca-uri si cum putem construi arborele comprimat. In prima faza vom liniariza arborele iar pentru fiecare query vom sorta lista celor nr noduri dupa pozitia in liniarizare. Lca-urile cautate sunt chiar lca-urile intre 2 noduri consecutive dupa sortare. Dupa ce am adaugat intr-un vector toate nodurile de interes (lca-uri plus nodurile din input) le vom sorta tot dupa aparitia acestora in liniarizare. Pentru construirea arborelui ne vom folosi de o stiva. Initial vom adauga in stiva primul nod din vector care, de fapt, este si radacina noului arbore. Apoi parcurgem vectorul sortat incepand de la pozitia a 2 a si cat timp first [ nodul curent ] nu se afla in intervalul ( first [ top ], last [ top ] ) stergem elemntul din varful stivei ( first [ nod ] si last [ nod ] sunt prima respectiv ultima aparitie din liniarizare a subarborelui lui nod ). Tatal nodului curent fiind, de fapt, varful stivei. Apoi inseram nodul curent in stiva.
Pentru rezolvarea update-ului ne vom folosi de un AIB. Daca valoarea muchiei intre nod si tatal lui nod este val atunci facem un update in AIB pe pozitia first [ nod ] cu val si pe pozitia last [ nod ] +1 cu –val. Pentru determinarea costului de la radacina la nod vom face un query in AIB pe pozitia first [ nod ].
Hektor
Graful fiind orientat aciclic, putem face o sortare topologica pe el. Vom nota cu expected [ nod ] = costul mediu cu care putem ajunge in nodul nod, pornind din nodul B si considerand toate drumurile fezabile. In z vom mentine sortarea topologica in ordine inversata. Cand ne aflam la un nod y, acesta produce costul cost [ y ] cu probabilitate de 1.0. Vom numara nodurile cu care are muchie directa orientata, care duc spre nodul B. Evident, expected [ y ] va fi egal cu cost [ y ] + suma din expected [ x ] / nr_noduri_bune, unde x este un vecin al lui y, iar nr_noduri_bune este numarul de noduri vecine cu y care au expected [ x ] diferit de 0.
De remarcat este faptul ca sortarea topologica ne garanteaza ca pentru un nod y, toate valorile expected [ x ], cu x vecin al lui y vor fi procesate inainte de procesarea valorii expected [ y ].
for ( auto y : z ) {
double sum = 0 ;
int nr = 0 ;
for ( auto x : gr [ y ] ) {
if ( expected [ x ] ) {
sum += expected [ x ] ;
++ nr ;
}
}
if ( nr ) {
expected [ y ] = sum / nr + cost [ y ] ;
}
}Lian Yu
Problema cere costul minim selectarii a K noduri cu proprietatea ca orice nod, inafara de cele K, l-am elimina cele K noduri selectate raman conexe. O prima observatie este ca putem alege oricum niste noduri dintr-o componenta biconexe, deoarece aceasta este definitia unei componente biconexe: orice nod am elimina celelalte raman conexe. O alta observatie este aceea ca daca vrem sa luam 2 noduri care se afla in 2 componente biconexe diferite legate printr-un nod critic suntem obligati sa luam si nodul critic. Deci ideea de rezolvare ar fi sa ne construim arborele biconexelor si sa aplicam o dinamica de tip rucsac pe acesta.Dinamica ar fi d [ nod ] [ k ] = costul minim sa selectam k noduri din subarborele lui nod care sa-l contina pe nod si sa fie conectate ( adica cele k noduri sa formeze un subarbore din subarborele lui nod ). Recurenta iese foarte usor, cum se poate observa si in acest cod:
for ( fiu din lista de fii )
for ( i = K ; i >= 0 ; i-- )
for ( j = K ; j >= 1 ; j-- )
d [ nod ] [ i + j ] = min ( d [ nod ] [ i + j ], d [ nod ] [ i ] + d [ fiu ] [ j ] ) ;int s = 0 ;
for ( fiu din lista de fii )
{
for ( i = min ( K, s ) ; i >=0 ; i-- )
for ( j = min ( K - i, size [ fiu ] ) ; j >= 1 ; j-- )
d [ nod ] [ i + j ] = min ( d [ nod ] [ i + j ], d [ nod ] [ i ] + d [ fiu ] [ j ] ) ;
s += size [ fiu ] ;
}Unde cu size [ nod ] am notat numarul de noduri din subarborele lui nod.
Voi demonstra in continuare ca, codul de mai sus are complexitate O ( N2 ) per total.
Voi nota numarul total de operatii facute ca sa rezolv tot subarborele lui nod cu f ( nod ) iar cu P ( nod ) afirmatia ca f ( nod ) <= size [ nod ]2.
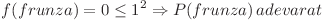
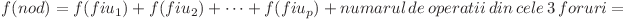
![=f(fiu_1)+f(fiu_2)+\dots+f(fiu_p)+size[fiu_1]+(1+size[fiu_1])*size[fiu_2]+(1+size[fiu_1]+
=f(fiu_1)+f(fiu_2)+\dots+f(fiu_p)+size[fiu_1]+(1+size[fiu_1])*size[fiu_2]+(1+size[fiu_1]+](https://www.infoarena.ro/static/images/latex/39eb4af438ba2a477687ff3652e5c53e_3.86108pt.gif)
![+size[fiu_2])*size[fiu_3]+\dots+(1+size[fiu_1]+size[fiu_2]+\dots+size[fiu_{p-1}])*size[fiu_p]=
+size[fiu_2])*size[fiu_3]+\dots+(1+size[fiu_1]+size[fiu_2]+\dots+size[fiu_{p-1}])*size[fiu_p]=](https://www.infoarena.ro/static/images/latex/e6e0967d213731100bf3bc4a51f92592_3.86108pt.gif)
![=\displaystyle\sum_{i=1}^{p} {f(fiu_i)}+\displaystyle\sum_{i=1}^{p} {size[fiu_i]}+\displaystyle\sum_{1\le i<j\le p} {size[fiu_i]*size[fiu_j]
=\displaystyle\sum_{i=1}^{p} {f(fiu_i)}+\displaystyle\sum_{i=1}^{p} {size[fiu_i]}+\displaystyle\sum_{1\le i<j\le p} {size[fiu_i]*size[fiu_j]](https://www.infoarena.ro/static/images/latex/8f0533e03de31224e3b99c7fc86d19bb_15.3261pt.gif)
![size[nod]^2=(1+size[fiu_1]+size[fiu_2]+\dots+size[fiu_p])^2=
size[nod]^2=(1+size[fiu_1]+size[fiu_2]+\dots+size[fiu_p])^2=](https://www.infoarena.ro/static/images/latex/591af9f7c883e8244cf84f74a81e6573_3.86108pt.gif)
![=1+\displaystyle\sum_{i=1}^{p} {size[fiu_i]^2}+2*\displaystyle\sum_{i=1}^{p} {size[fiu_i]}+2*\displaystyle\sum_{1\le i<j\le p} {size[fiu_i]*size[fiu_j]
=1+\displaystyle\sum_{i=1}^{p} {size[fiu_i]^2}+2*\displaystyle\sum_{i=1}^{p} {size[fiu_i]}+2*\displaystyle\sum_{1\le i<j\le p} {size[fiu_i]*size[fiu_j]](https://www.infoarena.ro/static/images/latex/818ea1f85e467a90d98efcfd9462cba2_15.3261pt.gif)
![Comform\,P(fiu_i),\,cu\,1\le i \le p \Rightarrow f(nod) \le size[nod]^2 \Rightarrow P(nod)\,adevarat
Comform\,P(fiu_i),\,cu\,1\le i \le p \Rightarrow f(nod) \le size[nod]^2 \Rightarrow P(nod)\,adevarat](https://www.infoarena.ro/static/images/latex/ea432ab50f026bb95e1cbbd7ebaa86ad_3.5pt.gif)
PscArb
Nu exista solutie pentru K > 2 si vom demonstra asta. Fie un nod aleator care nu e frunza si il vom considera radacina. Presupunem ca radacina nu e colorata R (celalalt caz se trateaza analog). Notam 3 frunze cu a, b si c. Fie R[x] = numarul de noduri colorate R de la radacina pana la nodul x. Daca R[a] + R[b] si R[a] + R© sunt impare atunci R[b] + R© + 2 * R[a] e par, deci si R[b] + R© e par. Deci, nu exista solutie.
Ramane cazul K = 2. In acest caz, arborele va fi un lant. Deoarece fiecare dintre cele 3 culori trebuie sa apara de un numar impar de ori, exista solutie doar daca N este impar. O posibila colorare este RGBBB...
