Teoria jocurilor
(Categoria Teoria jocurilor, Autor Filip Cristian Buruiana)
- Capitole
- Notiuni de baza
- Jocul NIM
- Numere Sprague-Grundy
- Adunarea jocurilor
- w-numere
- Aplicatii si probleme
Numere Sprague-Grundy
Alaturi de jocul NIM, numerele Sprague-Grundy au o importanta deosebita in analiza jocurilor impartiale. Majoritatea acestora se poate reduce la urmatorul joc: "Se considera un graf orientat aciclic care contine un pion intr-un nod oarecare. Cei doi jucatori muta alternativ. Prin mutare se intelege miscarea pionului din nodul in care se afla intr-un nod adiacent. Jucatorul care nu mai poate muta pierde."
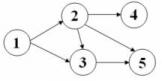
De exemplu, pentru graful din figura alaturata, daca pionul se afla initial in nodul 1, primul jucator aflat la mutare va pierde in cazul unui joc perfect.
Cum graful este aciclic, jocul este finit si are intotdeauna un castigator. Daca in graf exista un singur pion, castigatorul poate fi determinat prin metoda programarii dinamice. Astfel, winx va fi true daca si numai daca primul jucator aflat la mutare are strategie de castig atunci cand pionul se afla in nodul x. Astfel, winx = true daca si numai daca exista un nod y astfel incat sa existe arc intre x si y si winy = false. In caz contrar, winx = false. Pentru exemplul de mai sus, win2 = true, iar win1 si win4 vor fi false. Valorile vectorului win se vor calcula in ordinea din sortarea topologica a nodurilor, in complexitate O(N + M), unde N este numarul de noduri iar M numarul de muchii din graful dat.
Totusi, daca in graf ar exista mai multi pioni, problema determinarii castigatorului nu mai poate fi rezolvata prin programare dinamica. Folosind teoria dezvoltata independent de Roland Percival Sprague (1936) si Patrick Michael Grundy (1939), putem reduce complexitatea jocului cu mai multi pioni la complexitatea analizei jocului cu un pion. Ca in algoritmul de programare dinamica de mai sus, se incearca determinarea pozitiilor castigatoare si a celor necastigatoare pentru un singur pion.
Definitie: Functia Sprague-Grundy pentru un graf G = (V, E) este o functie mex (minimum excludant) definita pe V cu valori in multimea numerelor naturale, unde mex(x) = minim(n ≥ 0 |n diferit de mex(y), oricare ar fi y vecin al lui x).
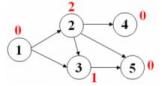 Altfel spus, valoarea Sprague-Grundy pentru un nod x al grafului aciclic dat este cel mai mic numar natural care nu este atribuit niciunui vecin al nodului x. Atribuirea valorilor se face incepand cu nodurile terminale, carora le este asociata valoarea 0. Valorile Sprague-Grundy pentru nodurile grafului de mai jos sunt scrise cu rosu in dreptul fiecarui nod.
Altfel spus, valoarea Sprague-Grundy pentru un nod x al grafului aciclic dat este cel mai mic numar natural care nu este atribuit niciunui vecin al nodului x. Atribuirea valorilor se face incepand cu nodurile terminale, carora le este asociata valoarea 0. Valorile Sprague-Grundy pentru nodurile grafului de mai jos sunt scrise cu rosu in dreptul fiecarui nod.
Se observa ca pozitiile care au valoarea Sprague-Grundy egala cu 0 sunt pierzatoare, in timp ce restul pozitiilor sunt castigatoare. Aceasta inseamna ca daca mex(x) = 0, in jocul cu un singur pion situat in nodul x jucatorul care muta primul nu are strategie sigura de castig, iar daca mex(x) este diferit de 0 atunci jucatorul care muta primul va castiga intotdeauna, in cazul in care joaca optim. Aceasta afirmatie este usor de demonstrat: daca mex(x) este diferit de 0 atunci exista un nod y, vecin al lui x, astfel incat mex(y) sa fie egal cu 0. In consecinta, primul jucator il va aduce intotdeauna pe adversarul sau in noduri care au valoarea Sprague-Grundy egala cu 0. Mai mult, primul jucator va ramane intotdeauna in noduri cu valoare diferita de 0, deoarece al doilea jucator nu il poate forta sa ajunga in aceste noduri: din nodurile cu valoarea 0 se poate ajunge doar in noduri cu valoarea nenula. In concluzie, jucatorul al doilea va pierde, deoarece va fi adus intr-un nod final (fara urmasi). La o analiza mai atenta se observa ca starile de joc respecta proprietatile pozitiilor castigatoare si pierzatoare, enuntate aici.
Valorile Sprague-Grundy se pot calcula si pentru jocuri in care nu apar precizate explicit grafuri. Fiecare stare posibila a jocului va fi un nod in graf, iar un arc va indica o posibila mutare: o trecere de la o stare la alta, conform regulilor existente.
Notiuni de baza | Jocul NIM | Numere Sprague-Grundy |
Adunarea jocurilor | w-numere | Aplicatii si probleme
