Solutii Junior Challenge 2015, Rundele 1 si 2

Vagoane

Functia Dubioasa

O metoda de rezolvare ar fi sa grupam fiecare numar cu un altul mai mic decat el respectand urmatoarele conditii:
1) Daca ambele numere au cel mai semnificativ bit pe aceeasi pozitie p, xorul lor va fi mai mic decat ambele cu cel putin 2^p, pentru ca dispare sigur acel bit p.
2) Bitul cel mai semnificativ al celui de-al doilea numar trebuie sa fie pe o pozitie pe care si primul numar are bitul setat 1, pentru ca xorul lor sa fie mai mic strict decat a si mai mare decat b.

Deci cea mai simpla metoda de constructie ar fi sa grupam fiecare numar (x) cu oricare altul (y) dintre cele care au bitul cel mai semnificativ pe pozitia pe care x are cel de-al doilea bit semnificativ. Daca nu mai exista un numar y neluat de alta valoare, atunci x va ramane negrupat.

Cu calu' la JBOI

Problema cere construirea unui sir de mutari de cal astfel incat sa nu se treaca de mai multe ori prin aceeasi casuta, sirul de mutari sa fie cat mai lung, si este de preferat sa plece dintr-un colt si/sau sa se termine intr-un colt. Vom incepe prin a explica solutia de 100, si apoi vom explica si cateva euristici sau solutii partiale, data fiind natura problemei, fiind acceptate si solutii cu drum neoptim.

  • Drumul pe care il vom prezenta trece prin toate casutele, fiind evidet, astfel, ca este optim. Ideea de baza consta in a observa ca putem imparti tabla in niste dreptunghiuri mai mici (care vor fi precalculate cu un back sau de mana), care pot fi unite inteligent astfel incat sa nu ramana vreo casuta nevizitata si sa se plece si sa se ajunga intr-un colt. Solutia uneste mai multe fasii (de latime fixa, mica) care trec prin doua tipuri diferite de blocuri. Primul tip, care apare exact odata in fiecare fasie, va fi notat cu INIT, iar cel de-al doilea tip de bloc va fi notat cu PAS. Fasiile vor fi construite astfel incat sa se termine intr-un colt al fasiei si sa plece fie din coltul opus, fie dintr-o casuta in care se poate sari din casuta de deasupra coltului opus. Pentru simplitatea vom considera ca se pleaca de undeva din stanga-sus si se ajunge in coltul dreapta jos, aceasta fasie putand fi rotita. De asemenea, vom considera ca aceasta fasie este indreptata inspre dreapta. Iata doua exemple de fasii, prima incepand din colutul stanga sus iar cealalta incepand dintr-o casuta in care se poate sari din casuta de deasupra coltuui stanga-sus:

  • Fasiile au, deci, o latime constanta, egala cu latimea lui INIT si cea a lui PAS care sunt practic niste matrice de mutari. In solutia noastra, ne folosim de fasii cu latimea 3 si 5. Astfel, se poate obtine prin alaturarea acestora orice latime naturala de la 8 in sus. Va trebui sa precalculam PAS-ul pentru fasiile de latime 3 si pentru cele de latime 5, PAS putand fi folosit indiferent de lungimea fasiei. Putem observa practic ca exista matrice PAS cu proprietatile necesare de lungime 4 atat pentru 3 , cat si pentru 5. Practic constructia unei fasii se realizeaza in mod inductiv, plecand de la matricea INIT. Pentru o fasie de o latime fixata($3$ sau 5) o sa avem nevoie de INIT-uri care au lungimi ce dau toate resturile posibile la impartirea cu 4(odata ce putem construi o fasie de lungime K, putem construi si de lungime K + 4, K + 8, etc, deci este suficient si necesar sa gasim INIT-uri care dau restul 0, 1, 2 sau 3 la impartirea cu 4).De asemenea, pe langa faptul ca trebuie sa avem INIT-uri care dau fiecare rest posibil la impartirea cu 4, trebuie sa avem doua pentru fiecare rest: unul care pleaca din coltul stanga-sus (imaginea 1) si unul care pleaca dintr-o casuta in care se poate sari din casuta de deasupra coltului stanga-sus (imaginea 2). Pentru a explica mai usor, sa notam fasiile care pleaca din coltul stanga-sus INIT_11. Pentur cel care pleaca dintr-un patrat in care se poate sari din casuta de deasupra coltului stanga-sus (practic patratul de coordonate 0, 1) le vom nota INIT_01 si vom considera ca ele chiar pleaca din casuta (0, 1), numai ca nu o consideram ca fiind in drum (practic e pozitia 0). Vom avea de precalculat 4 (lungimea INIT-ului trebuie sa dea fiecare rest la impartirea cu 4) * 2 (INIT_01 si INIT_11) * 2 (latime 3 si latime 5) + 2 (PAS-ul atat pentru 3, cat si pentru 5) = 18 matrice. Pentru cele de latime 3, vom precalcula INIT-uri cu lungimile 8, 9, 10 si 11, iar pentru cele de latime 5, vom precalcula INIT-uri cu lungimile 5, 6, 7 si 8.
  • Mai ramane de vazut cum unim fasiile astfel incat traseul sa ramana continuu. La modul general, solutia va arata in felul urmator:

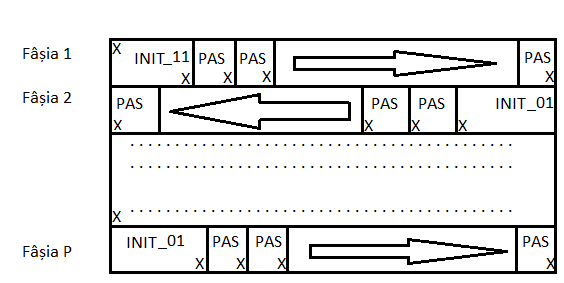
  • Cu alte cuvinte, fasiile impare sunt intreptate inspre dreapta, iar cele impare inspre stanga. Toate fasiile, cu exceptia fasiei 1, utilizeaza un INIT_01, iar fasia 1 incepe cu INIT_11. Drumul se va termina intr-un colt de jos, care este fie in stanga, fie in dreapta depinzand de paritatea lui P (numarul de fasii)
    PS Am notat cu X pasii intermediari prin care se trece la trecerea dintr-un bloc in altul.

Valuare

Cerinta problemei este simpla, si anume gasirea valorii numarului 123...(B-1) (considerat in baza B) modulo P. Solutia de 20 de puncte(subtaskul 1) este destul de usor de implementat, ideea ei de baza fiind cea a brutului.
Solutia pentru subtaskul 2, se bazeaza pe analizarea matematica a cerintei. Rescris matematic, numarul de mai sus arata in felul urmator:
S = 1 * B(B - 2) + 2 * B(B - 3) + ... + (B - 1) * B0
In urma unor calcule, reiese ca \documentclass[14pt]{report} S = \frac{B^B-B^2+B-1}{(B - 1)^2}
Pentru obtinerea a 20 de puncte (subtaskul 2) este suficient sa facem inversul modular pe baza micii Teoreme a lui Fermat, deoarece avem garantia ca P este prim si suficient de mare cat 2 sa nu fie divizibil cu acesta.
Pentru obtinerea a inca 20 de puncte (subtaskul 3) este suficient sa facem inversul modular utilizand indicatorul lui Euler sau algoritmul lui Euclid extins, dat fiind faptul ca gcd (B - 1, P) = 1 deci si gcd ((B - 1)2 , P) = 1
Pentru obtinerea a cel putin 80 de puncte, este necesara schimbarea strategiei si o mica observatie. Si anume, ca daca stim niste valori, putem uni doua numere. De exemplu, sa consideram B = 10 si P dat. Putem nota cu A numarul 123, B numarul 111 si C numarul 1000 (toate considerate in baza B + 1 = 10)
Astfel puetm scrie numarul ca fiind 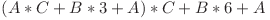(A * C + B * 3 + A) * C + B * 6 + A. Cu alte cuvinte, din numarul curent de lungime L, putem sari la numarul de lungime L + 3, inmultind numarul vechi cu C (egal cu B3 ) apoi adaugand B * L si din nou A. Solutia aceasta poate fi generalizata, putand adauga cate 100 sau cate 1000 sau, la cazul general, cate K cifre. Putem face precalcularile pentru valorila A, B, C, exact cum facem brutul in O (K) iar apoi punem cate K cifre la sfarsitul numarului cat timp se poate, restul de maxim K - 1 adaugandu-le cu brut. Astfel, se mai adauga la complexitate O (B / K + K), complexitatea totala devenind O (B / K + K), astfel observandu-se ca e optim sa alegem K = sqrt (B), obtinand complexitatea O (sqrt (B)). O astfel de solutie este oarecum similara cu brutul si obtine 80 de puncte.
Solutia de 100 se bazeaza pe observatia anterioara, si anume faptu ca putem uni doua numere. Astfel, reies doua solutii:

  • precalcularea numerelor de forma 123...K, 111...1 (de K ori) si 100...0 (de K ori 0) pentru K puteri de 2 si apoi concatenarea acestora in functie de scrierea in baza 2 a numarului B - 1, obtinandu-se complexitate log (B)
  • implementarea a 3 functiie toate primind parametru L:
    • functia get_pow (L) care returneaza numarul 100...0 (de L ori 0) modulo P. Acesta functie calculeaza practic BL modulo P, iar impplementarea ei se poate face recursiv, similar cu implementarea ridicarii la putere in timp logaritmic.
    • functie get11 (L) care returneaza numarul 11...1 (de L ori 1) modulo P. Aceasta functie se poate implementa tot recursiv (cand L este par, se imparte numarul in doua si se apeleaza get11 (L / 2) si get_pow (L / 2), iar cand L este impar se apeleaza get11 (L - 1)), astfel obtinandu-se complexitatea log2(B)
    • functie solve (L) care returneaza numarul 123...L (in baza B) modulo P. Aceast functie se implementeaza tot recursiv apeland functiile solve, get11 si get_pow, obtinandu-se o complexitate de log3(B)

Rayman

In primul rand, sa rezolvam problema pentru N = 1. Pentru ca lui Rayman nu-i place sa se intoarca din drum, inseamna ca trebuie sa gasim o insiruire de munti cu indicii crescatori, inaltimile descrescatoare si riscul total minim. Acesta este chiar subsirul maximal descrescator (care se poate rezolva cu AIB sau cu cautare binara in MlogM) cu o mica diferenta: in loc de o valoare, trebuie tinuta o pereche de valori, prima fiind lungimea subsirului, iar a doua riscul total. Trebuie maximizata prima valoare, iar in caz de egalitate trebuie minimizata a doua.
Printr-o analiza mai atenta la modul in care defineste Rayman “intoarcerea din drum”, reiese ca Rayman nu se poate intoarce din drum pe o linie, deci el poate sari de pe muntele (x1,y1) pe muntele (x2,y2) chiar daca y1 > y2. Asta inseamna ca noi putem “combina” subsirurile maximale descrescatoare de pe fiecare linie. Pentru subtaskul 3, deoarece E[i][j] = 0, putem doar sa aflam cardinalul subsirului maximal descrescator si riscul acestuia de pe fiecare linie si sa facem suma acestor valori. Pentru subtaskul 1 trebuie sa construim subsirul maximal descrescator propriu-zis, ca apoi sa le “unim” (acest lucru se poate face prin punerea tuturor subsirurilor intr-un vector si sortarea acestuia descrscator dupa inaltime) si sa calculam energia consumata (pentru acest subtask este de ajuns sa facem subsirul maximal descrescator in M2 prin dinamica clasica).
Pentru subtaskurile 2 si 4 intervine o problema: in vectorul in care s-au “unit” subsirurile maximale descrescatoare de pe fiecare linie apar subsecvente de munti cu aceeasi inaltime. In aceste subsecvente Rayman poate sari de pe orice munte pe oricare altul. Putem sa retinem o dinamica d[i][j] = energia minima pentru a parcurge muntii pana la i inclusiv si ultimul munte parcurs se afla pe linia j. Este suficient sa retinem aceasta dinamica pentru acei i care sunt ultima pozitie a fiecarei subsecvente. In cazul in care intr-o subsecventa se afla mai multi munti care apartin aceleiasi linii atunci e de ajuns sa pastram doar un munte, datorita restrictiilor: E[i][i] = 0 si E[i][j] ≤ E[i][k] + E[k][j], oricare ar fi k. Deci am redus fiecare subsecventa la munti care apartin de linii diferite doua cate doua. Aceste subsecvente se pot rezolva cu backtracking care e suficient pentru subtaskul 2, sau printr-o dinamica pe biti pentru subtaskul 4. O sa explic ce inseamna dinamica pe biti: d[mask][i][j] = energia minima daca in subsecventa avem munti care apartin liniilor corespunzatoare bitilor 1 din mask si sirul de mutari incepe cu muntele de pe linia i si se termina cu muntele de pe linia j. Aceasta dinamica se preproceseaza inainte de rezolvarea propriu-zisa.
Complexitate: N * MlogM + 2N * N3 + Nr subsecv * Lung subsecv2 (sau Nr subsecv * Lung subsecv3, depinde de implementare).

Cu mainile curate