Flori5
Fiecare floare necesită un disc central şi cel puţin K discuri exterioare.
Observaţie: nu are rost să folosim mai mult de K discuri în cadrul unei flori. Un număr de discuri care depăşeşte K nu îmbunătăţeşte numărul total de flori. Din contră, florile formate în viitor ar putea fi restricţionate din această cauză.
În continuare, împărţim problema în două părţi:
- Formăm cât mai multe grupe de exact K discuri de aceeaşi culoare, pe care le vom folosi apoi ca părţi exterioare ale florilor. Notăm numărul de grupe formate cu S.
- Fiecare grupă creată la pasul anterior necesită un disc central, de orice culoare. Putem folosi ca discuri centrale toate discurile rămase ca surplus în urma pasului anterior. Notăm numărul de discuri rămase cu C.
Acum trebuie să asociem fiecărei din cele S grupe câte unul din cele C discuri centrale.
Trebuie să tratăm 3 cazuri:
- S = C
În acest caz, există o potrivire perfectă între cele două mulţimi. Astfel, nu rămâne niciun disc nefolosit. Răspunsul va fi sol = S = C. - S < C
În acest caz, avem suficiente discuri centrale pentru a asocia câte unul fiecărei grupe din cele S. Rămân totuşi unele discuri centrale nefolosite. Având în vedere faptul că am început prin construcţia unui număr maxim de grupe exterioare, avem certitudinea că nu vor rămâne suficiente discuri suplimentare pentru a crea o floare nouă. Răspunsul va fi sol = S. - S > C
În acest caz, am creat prea multe grupe exterioare, şi nu avem suficiente discuri centrale pentru a finaliza toate florile. Pentru a repara daunele, putem proceda în următorul fel:- Alegem un grup exterior de K discuri, din cele S formate.
- Îl distrugem.
Fiecare execuţie a paşilor 3.1 – 3.2 ne afectează cantităţile existente: numărul de grupe exterioare scade cu o unitate, în timp ce numărul de discuri centrale creşte cu K.
Putem repeta procesul descris anterior până când cantităţile S şi C se echilibrează. Acest procedeu poate fi simulat pas cu pas, sau aplicând o căutare binară. Astfel de soluţii obţin 60-70p. Pentru 100p, trebuie să aflăm soluţia în timp constant, pe cale matematică.
În plus, trebuie luat în considerare calculul valorilor S şi C pentru fiecare din cele M întrebări. Aceste valori pot fi calculate în timp liniar, pentru 60-70p, sau în timp constant, folosind sume parţiale. Soluţia din urmă obţine punctaj maxim.
Complexitate: O(N + M).
Findmin
Soluţia 1 - O(N) - 100 de puncte - Răzvan Sălăjan
Se sortează crescător (în O(N)) cele N valori, reţinând şi poziţiile iniţiale. Se observă că pentru fiecare element din vectorul sortat ne interesează cel mai mic indice din partea stângă (având în vedere faptul că elementele sunt sortate crescător, e evident că toate cele din stânga sunt mai mici).
Fie j cel mai mic indice. Daca j este mai mic decât indicele elementului curent în vectorul iniţial, atunci soluţia e j, altfel e -1.
Soluţia 1.1 - O(NlogN) - 70 de puncte - sortarea se face in O(NlogN).
Soluţia 2 - O(N) - 100 de puncte - Răzvan Sălăjan
Se parcurg elementele vectorului în ordinea dată. Fie P[i] valoarea curentă. Se marchează toate valorile de la P[i]+1 până la N ca având soluţie poziţia i. Dacă întâlnim un element care a fost deja marcat, ne oprim.
Dacă P[i] nu a fost marcat până la pasul curent, atunci soluţia e -1. Având în vedere că ne oprim de fiecare dată când un element a fost deja marcat, fiecare element va fi marcat doar o singură dată.
Soluţia 3 - O(NlogN) - 70 de puncte – Sergiu Puşcaş
Se parcurg elementele vectorului în ordinea data. Fie ST[] o stivă. În stivă vom introduce valori în felul următor:
• dacă valoarea din vârful stivei e mai mare decât valoarea elementului curent, introducem valorea curentă în stivă (soluţia pentru elementul curent e -1).
• altfel, vom căuta binar în stivă cel mai din stânga element care are valoarea mai mică decât P[i], iar elementul curent nu va fi introdus în stivă (vârful stivei e şi mai la stânga, şi mai mic decât elementul curent, deci elementul curent nu va fi folosit niciodată în viitor).
Se observă că elementele din stivă sunt în ordine descrescatoare după valoare şi în ordine crescătoare după poziţie, deci poate fi aplicată cautarea binară.
Soluţia 4 - O(N2) - 40 de puncte - Răzvan Sălăjan
Se parcurg elementele vectorului în ordinea dată. Pentru fiecare element se caută printre cele i-1 poziţii cea mai din stânga poziţie care are valoarea mai mică decât P[i].
NN
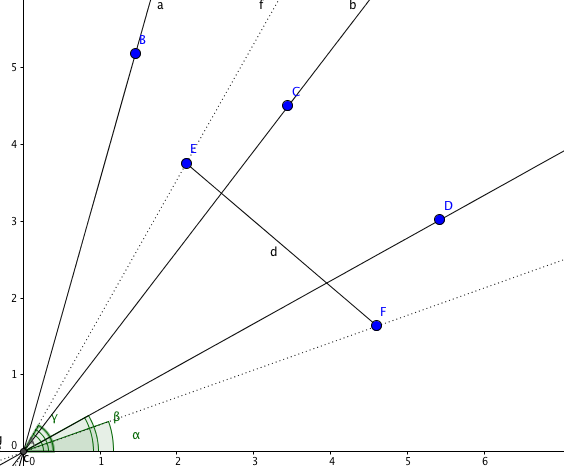
În descrierea soluţiei, segmentele sunt reprezentate de barajele din problemă, iar semidreptele sunt malurile date. De asemenea, vom considera unghiul polar al unei drepte ca fiind unghiul dintre dreaptă şi axa de coordonate Ox.
Pentru a rezolva problema, va trebui sa găsim o mulţime maximală de semidrepte consecutive tăiate de un segment. Observăm că acestea au unghiul polar cuprins între cele 2 unghiuri polare ale semidreptelor care pleacă din origine şi conţin câte un capăt al barajului.
O idee de rezolvare care rulează în O(logN) pentru fiecare segment dat e să sortăm, de la început, toate semidreptele în funcţie de unghiul polar. De asemenea, notăm cu s1 semidreapta care conţine unul dintre capetele segmentului dat şi are unghiul polar mai mic, respectiv cu s2 semidreapta care conţine celălalt capăt. Dorim să calculăm numărul de semidrepte cu unghiuri polare cuprinse între unghiul polar al semidreptei s1 şi cel al semidreptei s2.
Deoarece semidreptele sunt deja sortate după unghiul polar, rămâne doar să căutăm binar semidreapta cu cel mai mic unghi polar >= unghiul polar al lui s1 şi semidreapta cu cel mai mare unghi polar <= unghiul polar al lui s2. Soluţia va fi diferenta dintre indicii celor două semidrepte găsite în şirul sortat după unghiul polar.
În calcule, pentru o precizie mai mare, se recomandă folosirea tipului de date long double. De asemenea, la calcularea unghiului polar se va încerca evitarea folosirii funcţiei atan2, care este mai lentă!
Marele Zgomot
Soluţia 1: O(N * M) - 100p
Pentru a afla numărul de circuite este suficient să facem o parcurgere în adâncime de fiecare dată când găsim o celulă nevizitată care aparţine unui circuit.
Observăm că pentru a uni două circuite, este necesar să trecem prin exact o zonă cu celule libere. Numim zonă cu celule libere o zonă în care putem ajunge de la o celulă la oricare alta prin alte celule care nu conţin circuite. Pentru fiecare zonă aflăm toate capetele circuitelor care se învecinează cu ea. Astfel vom şti pentru fiecare zonă care circuite pot fi unite prin ea. Pentru a forma un circuit de lungime maximă, vom alege cele mai lungi două circuite care se învecinează cu acea zonă. Soluţia va fi maximul dintre valorile obţinute prin însumarea perechii de circuite maxime găsite pentru fiecare zonă.
Pentru a reconstitui soluţia, vom reţine pe lângă lungimea fiecărui circuit adiacent zonei şi celula liberă vecină cu ea. Pentru a le uni, vom face o parcurgere în lăţime de la capătul primului circuit până la capătul celui de-al doilea circuit.
Soluţia 2: O((N * M)2) - 40p
Pentru a alege perechea de circuite care să fie unite, se poate lua fiecare capăt al fiecărui circuit şi aplica un algoritm de tip Lee/fill pentru a afla capetele circuitelor cu care se poate forma legătura.
Mapal
Presupunem că vrem să facem linia L palindrom. Fiecare element L[j] de pe linia L trebuie să fie egal cu L[N-j+1]. Astfel, pentru fiecare linie avem perechile de elemente egale cu indicii ((i, j), (i, N-j+1)).
În mod similar, pentru coloane vom avea perechile de elemente egale cu indicii ((i, j), (N-i+1, j)).
Astfel, vom avea maxim câte 4 elemente care trebuie să fie egale simultan. Dintre acestea, numărăm elementele egale cu 0 şi elementele egale cu 1 şi le schimbăm pe cele cu frecvenţa mai scăzută.
O sursă care aplică principiile de mai sus:
int n, q, rez, cnt[2], x;
string m[DN];
bitset<DN> viz[DN], l, c;
void dfs(int a, int b) {
++cnt[m[a][b]-'0'];
viz[a][b]=1;
if(c[b] && !viz[n-a-1][b]) dfs(n-a-1,b);
if(l[a] && !viz[a][n-b-1]) dfs(a,n-b-1);
}
int main() {
// citire n, m[], l[], c[]
for(int i=0; i<n; ++i)
for(int j=0; j<n; ++j)
if(!viz[i][j] && (l[i] || c[j])) {
cnt[0] = cnt[1] = 0;
dfs(i, j);
rez += min(cnt[0], cnt[1]);
}
// afişare rez
}Albume
Simularea repetată a experimentului – 0p
Putem simula experimentul folosind funcţiile random din C/C++ sau Pascal. Din cauza limitei de timp, putem obţine doar o aproximare a rezultatului. Lipsa preciziei duce la un scor de 0 puncte.
Brut - O(C*K * 2C*K) – 20p
Reprezentăm cele C*K albume sub forma unui şir binar de C*K biţi. Toţi biţii cu poziţia în aceeaşi clasă de resturi modulo C aparţin aceleiaşi formaţii.
Exemplu: C=4, K=3 -> 321032103210 (biţii aflaţi la poziţii din C în C reprezintă albume de la aceeaşi formaţie).
Există 2C*K configuraţii posibile. Le generăm pe toate şi le procesăm doar pe cele valide (care au exact Q biţi de 1).
Pentru o configuraţie validă, determinăm câte formaţii apar (formaţia x apare în configuraţie dacă există cel puţin un bit de 1 pe o poziţie care dă restul x la împărţirea cu C). Calculăm suma numărului de formaţii şi numărul total de configuraţii valide, soluţia fiind raportul lor.
Cazuri particulare – alte 20p
a) K = 1
Există un singur album de la fiecare formaţie.
Toate cele Q albume alese provin de la formaţii diferite.
La fiecare extragere se obţin exact Q formaţii.
Raspunsul e Q.
b) Q = C*K
Există C*K albume în total şi de fiecare dată se extrag toate.
Întotdeauna apar toate formaţiile.
Răspunsul e C.
Soluţia bună – O(K) – 100p
Notăm pi = probabilitatea să existe formaţia i printre albumele extrase.
Fiecare formaţie poate contribui (cu o probabilitate proprie) la numărul total de formaţii.
Numarul mediu de formaţii din setul extras e:
X = p1 + p2 + ... + pC
Cum calculam pi?
pi = probabilitatea să existe formaţia i
= 1 - (probabilitatea sa nu existe formaţia i)
= 1 - A / B
unde A = numărul de configuraţii de dimensiune Q care NU au formaţia i
B = numărul total de configuraţii de dimensiune Q
Pentru A avem o formaţie interzisă, deci C-1 formaţii permise. În total, K * (C-1) albume permise. Din ele alegem Q. Le putem alege în C(K * (C-1), Q) moduri.
Pentru B, avem toate cele C formaţii permise. În total, K * C albume. Din ele alegem Q. Le putem alege în C(K * C, Q) moduri.
În consecinţă, pi = 1 - C(K * (C-1), Q) / C(K * C, Q)
Observăm că probabilitatea unei formaţii nu depinde de formaţie. Cele C formaţii sunt simetrice şi avem p[1] = p[2] = ... = p[C]
Soluţia devine:
X = p1 + p2 + ... + pC
= C * p1
= C * (1 - A / B)
= C * (1 - C(K * (C-1), Q) / C(K * C, Q))
Expresia poate fi prelucrată matematic, folosind formula de calcul a combinărilor. O parte din factoriale se reduc. În cele din urmă, se ajunge la rapoartele
A = (K * C - K)! / (K * C)! -> are forma (1 / produs de K factori)
B = (K * C - Q)! / (K * C - Q - K)! -> are forma (produs de K factori)
X = A * B
Generăm pe rând câte un factor din A şi unul din B şi înmulţim soluţia curentă cu raportul celor 2 factori.
În acest fel, valorile intermediare nu ating valori foarte mari, cum ar fi în cazul în care calculăm valoarea exactă a numărătorului şi a numitorului.
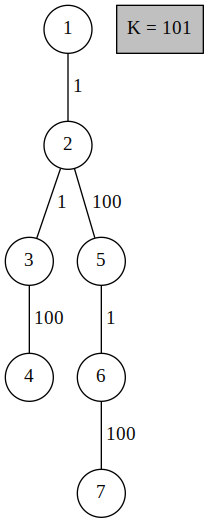
Rege2
Alex Cociorva: O(N^2 * log VALMAX) - 50 puncte
O să ne reconstruim arborele în mai mulţi arbori în felul următor: fiecare muchie devine un nod, iar fiecare nod devine o muchie. După această transformare, nodurile o să aibă costuri, muchiile nu.
Luăm ca exemplu arborele următor:

Acesta se va transforma în următorii 2 arbori:
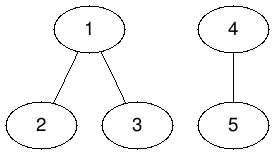
Costurile se vor transmite la noduri după cum urmează:
cost(1) = 10, cost(2) = 20, cost(3) = 30, cost(4) = 40, cost(5) = 50.
Problema s-a redus la a găsi un K minim astfel încât să putem acoperi arborele cu maxim S lanţuri formate din noduri, fiecare lanţ având cost cel mult K.
Observăm că putem căuta binar rezultatul. Pentru un K fixat, vrem să verificăm dacă putem acoperi arborele cu maxim S lanţuri de cost cel mult K.
Ne vom construi o dinamică pe arbore: dp[x] = numărul minim de lanţuri necesare pentru a acoperi subarborele ce are rădăcina în x, astfel încât fiecare lanţ să aibă cost cel mult K.
Dupa reconstruirea arborelului, vom avea P arbori noi. Fixăm pentru fiecare rădăcinile: r1, r2, ..., rp. Dacă dp[r1] + dp[r2] + ... + dp[rp] <= S, atunci am găsit o acoperire bună.
Să presupunem că vrem să calculăm dp[x]. O să încercăm să ne construim toate lanţurile posibile care încep din x şi au cost <= K. Putem face acest lucru cu un DFS din nodul x, vizitând toate nodurile y, cu y din subarborele lui x, astfel încât costul lanţului x->y să fie maxim K.
dp[x] = min(dp[x], 1 + suma(dp[z])), unde z este în subarborele lui x şi z este adiacent cu un nod de pe lanţul x->y.
În concluzie, pentru fiecare nod x va trebui să facem acest DFS. Cu o implementare atentă care menţine suma(dp[z]) pe parcurs ce face DFS-ul, obţinem o complexitate de O(N^2 * log VMAX), soluţie ce obţine 50 de puncte.
Cosmin Rusu: O(N * log VALMAX) – 100p
Se observă că dacă există o soluţie pentru un număr K, atunci orice K’ > K este, de asemenea, soluţie. Putem deci căuta binar răspunsul.
În continuare ne propunem să găsim numărul minim de lanţuri de lungime maxim K (fixat în căutarea binară) cu care putem acoperi întreg arborele.
O altă observaţie importantă este următoarea: orice frunză va fi acoperită de un lanţ format din minim două noduri (tata->frunza). Pe observaţia asta se bazează şi soluţia: pornim din frunze şi, la un anumit pas, dacă avem de ales între mai multe lanţuri începute, o să-l alegem pe cel de lungime minimă. În cazul în care un astfel de lanţ nu există, sau suma dintre lungimea lui şi lungimea noii muchii este mai mare decât K, acoperim noua muchie cu un nou lanţ. Dacă numărul de lanţuri este cel mult S, scădem K. Dacă nu, creştem K.
Menţionăm că alte greedy-uri care pornesc din rădăcină sunt greşite. Un contra-exemplu ar fi următorul: