Solutii Algoritmiada 2011, Runda 2

Derdelus

Problema se rezolva prin programare dinamica. Fie bst[i][j] numarul de moduri de-a ajunge in celula (i,j). Recurenta este destul de simpla, si anume bst[i][j] = Suma (bst[i - k][j]) + Suma (bst[i - k][j - k]) 1 ≤ k ≤ M.

Implementarea acestei solutii are o complexitate de O(N3) si nu obtine punctajul maxim. Pentru a reduce complexitatea la O(N2) se pot retine sumele partiale pe coloane si pe diagonale, si astfel se poate calcula bst[i][j] in O(1).

Raliu

Complexitate: O(N)

Fie L[i] = numarul de litri disponibili la benzinaria i si D[i] = distanta pana la benzinaria i + 1. Vom forma un nou vector V[i] = L[i] - D[i] pe care il dublam pentru a ne fi mai usor la implementare. Executam algoritmul de gasire a subsecventei de suma maxima pe vectorul V si alegem ca solutie prima subsecventa de lungime N cu suma pozitiva pe care o gasim.

Turnuri2

O solutie brute-force ar fi: pentru o cladire i, 1 ≤ i ≤ N verificam in stanga si respectiv dreapta coeficientul de frumusete maxim, cat timp avem cladiri de inaltimi mai mici.

Solutia optima pleaca de la soutia brute-force, cu o optimizare. Pentru o pozitie i, retinem pozitia j, cu semnificatia ca j este cel mai din stanga turn pe care il vad de pe turnul i. Daca am calculat pentru o cladire j coeficientul de frumusete maxim pe care il are, atunci pentru pasul curent i, mergem inapoi pe aceste pozitii, atata timp cat inaltimea acestor turnuri nu o depaseste pe cea curenta si luam maximul dintre acele coeficiente maxime.

Algoritmul in C++ pentru partea din stanga arata in felul urmator:

for ( int i = 1; i <= N; ++i) {
    maxi = K[i]; //maxi = coeficientul maxim pentru turnul i
    int j;
    for (j = i - 1; j > 0 && H[j] <= H[i]; j = poz[j] )
        maxi = max ( maxi, best[j] ) ;
    maxi = max ( maxi, K[j] ) ;

    best[i] = maxi ;
    poz[i] = j ;
}

Se executa algoritmul si pentru partea din dreapta, si se obtine solutia.

Drumuri3

Observam ca la aceasta problema ni se da un graf neorientat si ni se cere numarul de drumuri de lungime cel mult 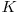K intre doua noduri date. Putem rezolva aceasta problema in felul urmator: determinam numarul drumurilor de lungime cel mult 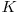K intre oricare doua noduri, apoi raspundem in timp constant la fiecare dintre cele 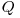Q intrebari.
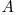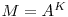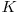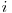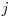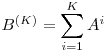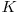Fie A matricea de adiacenta a grafului dat. Se stie ca o intrare M[i][k] din M = A^K reprezinta numarul de drumuri de lungime (unde lungimea unui drum se masoara in numarul de muchii, si nu de noduri de pe respectivul drum) exact K dintre nodurile i si j. De aici, avem ca B^{(K)} = \displaystyle\sum\limits_{i=1}^K A^i are ca intrari B[i][j] numarul de drumuri de lungime cel mult K din graful nostru. Daca calculam in mod direct matricea 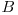B si raspundem in 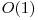O(1) la fiecare dintre cele 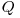Q intrebari, obtinem un algoritm de complexitate 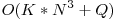O ( K * N ^3 + Q ); am presupus ca folosim algoritmul naiv de inmultire a doua matrici care ia 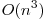O(n^3). Daca folosim algoritmi mai performanti de inmultire a matricilor putem obtine timpi mai buni, in particular cu algoritmul lui Strassen obtinem o complexitate de 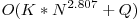O ( K * N ^ {2.807} + Q ) , dar niciunul dintre acesti algoritmi nu obtine punctaj maxim.

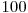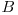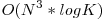Pentru a obtine 100 de puncte putem sa folosim un algoritm care determina matricea B in O( N ^3 * log K ) si care foloseste algoritmul naiv de inmultire a matricilor. Algoritmul pe care il voi descrie foloseste tehnica Divide et Impera si se bazeaza pe o mica observatie. Fie suma 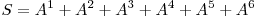S = A^1 + A^2 + A^3 + A^4 + A^5 + A^6. Aceasta poate fi scrisa 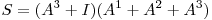S = ( A ^ 3 + I ) ( A ^ 1 + A ^ 2 + A ^ 3 ) daca dam factor comun pe 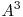A^3 si mai apoi pe 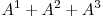A^1 + A^2 + A^3. Cum calculam suma pe cazul general? Calculam suma pentru prima jumatate a termenilor, apoi, folosindu-ne de similaritatea dintre cele doua jumatati, calculam suma si pentru cealalta jumatate a termenilor, iar la sfarsit adunam cele doua jumatati. Astfel obtinem urmatoarea relatie de recurenta:
B^{(K)} =\begin{cases} B^{(\frac{K}{2})}*(A^{\frac{K}{2}}+I),\quad K \quad par\ B^{(\frac{K-1}{2})}*(A^{\frac{K-1}{2}}+I) + A*(A^{(\frac{K-1}{2})})^2,\quad K \quad impar\ \end{cases}
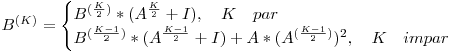
cu termenul initial 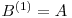B^{(1)}=A . Matricea 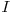I este matricea unitate. Putem implementa acest calcul recursiv sau nerecursiv, ambele variante obtinand 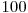100 de puncte. Algoritmul are complexitatea finala O( N ^3 * log K + Q).

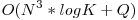Procesor

Solutia 1: O(N * logN)

Pentru inceput se sorteaza procesele descrescator dupa timpul T[i].
Apoi parcurgem momentele de timp de la T[1] la 1, si la pasul i, introducem intr-un max-heap ordonat dupa penalizare toate procesele j care au T[j] >= i. Apoi marcam procesul din varful heapului ca fiind executat si trecem la pasul urmator.

In final, adunam la solutie penalizarile proceselor neefectuate.

Culoar

Se disting doua cazuri:

  1. Fiecare din cele doua drepte cautate trece prin exact un punct. In acest caz cele doua drepte trebuie sa fie perpendiculare pe segmentul care uneste cele doua puncte.
  2. Cel putin una din drepte trece prin doua puncte. Avand fixata o dreapta care trece prin doua puncte ne intereseaza cele mai apropiate puncte fata de dreapta din fiecare semiplan.

In total avem O(N2) perechi de drepte candidate pentru solutie. Vom sorta aceste drepte in functie de panta si le vom parcurge in ordine. La fiecare pas ne vom mentine punctele sortate dupa panta dreptei curente. Atunci cand trecem de la o dreapta la urmatoarea se va schimba ordinea a cel mult 2 puncte consecutive.