Soluţii ONIS 2016, Runda 1

• Lista de probleme
• A. Consecutive
• B. Carte2
• C. Tribut
• D. Revolta
• E. Metrou4
• F. Robo
• G. Twoton
• H. Sate2
• I. Politie
• J. Pq
• K. Padure2

A. Consecutive

Vom privi din alt unghi ce inseamna ca un numar sa fie suma de mai multe numere naturale consecutive.

Avem N = Sum(x ... y) = Sum(1 ... y) - Sum(1 ... x - 1) = y * (y + 1) / 2 - x * (x - 1) / 2 = (y * (y + 1) - x * (x - 1)) / 2. Trecem N in 2 * N. Ecuatia devine 2 * N = y^{2 + y - x}2 + x. Descompunem diferenta de patrate si dam factor comun: 2 * N = (y - x) * (y + x) + (y + x) = (y + x) * (y - x + 1). Pentru simplitatea calculelor, vom defini Z = y + x. Atunci, forma finala e egalitatii va fi: 2 * N = Z * (Z - 2 * x + 1). Observam, deci, ca pentru fiecare divizor al lui 2 * N, fie acesta Z, exista maxim o pereche determinata de Z (x, y) astfel incat egalitatea sa fie satisfacuta. Vom parcurge fiecare divizor al lui 2 * N pana la sqrt(N) (inclusiv), adaugand intr-un vector perechile (d, 2 * N / d) pe care le intalnim, cu d divizor al lui 2 * N.

Acum am vrea sa "gasim" in fiecare pereche de mai sus (d, 2 * N / d) unicele x, y (daca acestea exista) astfel incat y + x = 2 * N / d si y - x + 1 = d. Ordinea trebuie sa fie aceasta, intrucat x < y si d < 2 * N / d. Rezolvand sistemul de ecuatii, obtinem posibila pereche solutie y = (d + (2 * N / d) - 1) / 2 si x = d - y. Memoram aceste perechi candidat.

Ramane doar de sortat perechile si de testat pentru fiecare in parte daca este, de fapt, solutie a problemei. Nu toate perechile vor fi solutii, deoarece exista cateva cazuri marginale precum cel in care 2 * N este patrat perfect.

Complexitate timp: O(sqrt(N) + sqrt(N)log(sqrt(N))).
Complexitate spatiu: O(sqrt(N)).

B. Carte2

O prima posibilitate este a incerca pe rand toate cele 6 * 2 configuratii si a vedea daca vreuna dintre ele se potriveste. Alternativ, pentru a reduce din "tractoreala", se pot sorta crescator ambele siruri, incat ramane de incercat o singura configuratie, alegand cele mai mari dimensiuni, de la sfarsitul sirului sortat.

C. Tribut

Vom aborda problema cu ajutorul tehnicii de Flux maxim. Astfel, construim o retea in care fiecare sistem solar i are asociat nodul i, iar fiecare uniune comerciala j nodul N + j. Sursa si destinatia vor fi alese convenabil astfel incat sa nu se suprapuna cu nodurile necesare. Vom trage un arc de la sursa la fiecare sistem solar i printr-o muchie de capacitate solarSystemTribute[i], cat si un arc de la fiecare planeta la fiecare dintre uniunile comerciale din care face parte, cu capacitate INFINIT. In final, tragem arcuri de la uniunea comerciala i la destinatie, de capacitate unionTribute[i]. Ramane sa rulam algoritmul de flux pe acest graf, iar fluxul maxim rezultant reprezinta solutia problemei.

Complexitate timp: O(N^5) (daca se implementeaza cu Edmonds-Karp, mai putin daca se foloseste push-relabel).
Complexitate spatiu: O(N^2).

D. Revolta

E. Metrou4

F. Robo

G. Twoton

Obesrvam ca functia adecvat denumita wtf(), odata apelata de la pozitia i, dupa un anumit numar de pasi se va intoarce la pozitia i si nu va mai ajunge niciodata la i + 1. De aici ne vine ideea de a calcula, pentru fiecare pozitie i, 0 <= i < N, doua valori: steps[i] = cati pasi face functia pana se intoarce in valoarea i si ret[i] = ce valoare returneaza wtf(i). Evident, steps[N - 1] = 1, iar ret[N - 1] = V[N - 1]. Parcurgem descrescator pozitiile, iar pentru pozitia i, 0 <= i < N - 1, vom calcula cele doua valori astfel: steps[i] se initializeaza cu 1 + steps[i + 1] (functia cheama la inceput wtf(i + 1)). Apoi, ne uitam la ret[i + 1]. Daca acesta este mai mare sau egal cu V[i], recursivitatea pe acest nivel se sfarseste, setam ret[i] = V[i] si continuam. Altfel, wtf(i + 1) se mai apeleaza odata, deci steps[i] += steps[i + 1], iar ret[i] = ret[i + 1]. Raspunsul se va gasi in steps [0].

Complexitate timp: O(N).
Complexitate spatiu: O(N).

Descrierea solutiei Stefan Ciobaca

Funcţia wtf calculeaza minimul din vector in timp exponential in cazul cel mai nefavorabil (cand minimul este pe ultima pozitie). Ce e interesant este ca functia nu este inventata: la un laborator de Programare Functionala, un student (bun) a scris, din greseala, o functie care calculeaza minimul dintr-o lista in timp exponential, similara cu functia C de mai jos.

Observam ca variabila count tine minte numarul de apeluri ale functiei wtf, modulo 19997.

int wtf(int i)
{
  count++;
  if (count >= 19997) {
    count -= 19997;
  }
  if (i == n - 1) {
    return a[i];
  }
  if (a[i] < wtf(i + 1)) {
    return a[i];
  } else {
    return wtf(i + 1);
  }
}

Pentru a rezolva problema intr-o complexitate buna, este necesar sa eliminam al doilea apel, redundant, la wtf(i + 1):

int wtf_better(int i)
{
  count++;
  if (count >= 19997) {
    count -= 19997;
  }
  if (i == n - 1) {
    return a[i];
  }
  int cache = wtf_better(i + 1);
  if (a[i] < cache) {
    return a[i];
  } else {
    return cache;
  }
}

In acest moment, am eliminat ineficienta, dar valoarea lui count nu mai este corecta (numara cate apeluri face functia wtf_better, nu wtf). Pentru a calcula valoarea corecta a lui count, este suficient sa tinem minte si un tablou memo[], unde memo[i] tine minte cate apeluri ar fi luat wtf(i):

int wtf_even_better(int i)
{
  memo[i] = 1;
  if (memo[i] >= 19997) {
    memo[i] -= 19997;
  }
  if (i == n - 1) {
    return a[i];
  }
  memo[i] += memo[i + 1]; // simulez primul apel la wtf(i + 1)
  if (memo[i] >= 19997) {
    memo[i] -= 19997;
  }
  int cache = wtf_even_better(i + 1);
  if (a[i] < cache) {
    return a[i];
  } else {
    memo[i] += memo[i + 1]; // simulez al doilea apel la wtf(i + 1)
    if (memo[i] >= 19997) {
      memo[i] -= 19997;
    }
    return cache;
  }
}

Rezultatul este in memo[ 0 ] dupa apelul la wtf_even_better(0).

Solutia de mai sus se poate obtine aproape mecanic, fara a intelege codul initial. Tot mecanic se poate obtine si solutia iterativa, care completeaza tabloul memo[] de la stanga la dreapta in timp ce calculeaza minimul din vector. Si solutia recursiva si cea iterativa pot fi vazute ca exemple simple de programare dinamica.

H.Sate2

Problema cere o partitionare in k subseturi a caror suma sa fie egala. Aceasta problema este NP completa. Considerand restictiile problemei, putem folosi metoda Greedy. Aceasta nu va gasi mereu rezultatul dorit, dar ne marim sansele daca rulam mai multe greedy-uri diferite si vedem daca macar una gaseste o partionare buna. O alta idee ar fi sa folosim metoda Monte Carlo, se extragem un element la intamplare din rucsacul cel mai greu si sa-l mutam in rucsacul cel mai usor, astfel incat sa nu depasim greutatea necesara fiecarui rucsac, si anume m / k, pana ne epuizam un numar de pasi stabilit prealabil sau am gasit o solutie.

Facand abstractie de la restrictiile problemei, rezolvam folosind metoda programarii dinamice pentru fiecare caz, k = 3: dp[i][j][p] = 1 sau 0 daca putem obtine, folosind primele i obiecte, o partionare astfel incat primul rucsac are greutatea j, al doilea greutatea p, iar evident al treilea va avea greutate m - j - p. Se procedeaza similar pentru cazul cu k = 4.

Toate solutiile mentionate iau punctaj maxim.

I. Politie

Observam ca politistii vor merge intai pe toate drumurile optime (dupa enunt) dintre nodurile legate direct sau indirect doar de muchii de categorie 1, dupa aceea doar de muchii de categorie <= 2, de categorie <= 3, etc. Impartim muchiile dupa categorie. Consideram la fiecare pas i, 1 <= i <= D, ca avem nodurile grupate in componente conexe astfel incat intre orice doua noduri din cadrul aceleasi componente conexe se poate ajunge mergand numai pe muchii de categorie strict mai mica decat i. Uitandu-ne la muchiile de categorie i, este posibil ca intre unele perechi de componente conexe sa fi "aparut" una sau mai multe muchii. Politistii vor dori sa faca drumuri de la orice componenta la orice alta folosind muchiile noi (atat cat se poate), avand grija sa aleaga de fiecare data un drum cu periculozitate maxima minima. Ne imaginam un graf, privind componentele deja stabilite ca pe noduri, si ca muchii intre ele doar muchiile originale de categorie i. Astfel, problema se reduce la a gasi un subset de muchii cu cost maxim minim astfel incat, dupa conectarea nodurilor lor aferente, intre orice doua noduri apartinand aceleeasi componente conexe din graful imaginat sa existe un drum - adica, un Arbore partial de cost minim. Sortam, deci, muchiile din categoria curenta crescator dupa periculozitate si aplicam algoritmul lui Kruskal, avand grija sa introducem intr-un vector toate periculozitatile muchiilor selectate. Procedeul se repeta pana am epuizat toate muchiile. La final sortam descrescator vectorul pe care l-am mentinut si afisam primele P elemente distincte.

Alternativ, mai simplu, putem pur si simplu sorta muchiile crescator dupa categorie, si in caz de egalitate crescator dupa periculozitate si, la sfarsit, sa aplicam Kruskal. Practic simulam procesul de deasupra.

Complexitate timp: O(MlogM + Mlog*N).
Complexitate spatiu: O(N + M).

J. Pq

Observam ca o pozitie nu poate lua parte in mai mult de doua perechi - altfel, conform principiului cutiei ar exista fie la stanga, fie la dreapta, doua elemente "cele mai apropiate si egale", o absurditate. Urmarind acelasi fir logic, concluzionam ca o celula poate fi capatul stang al maxim unei perechi, si capatul drept al maxim unei perechi. Ne vine ideea de a retine in fiecare capat dreapta al vreunei perechi distanta dintre elementele perechii. Vom sorta queryurile crescator dupa L si le vom rezolva interogand un arbore de intervale de maxim pe (L ... R). De asemenea, trebuie avut grija ca, atunci cand capatul L curent se misca la dreapta, toate perechile peste a caror capat stang am trecut sa fie scoase din arbore - suprascrise cu 0. Parcurgem de la stanga la dreapta vectorul, retinand pentru fiecare valoare lastOccurrence[i] = ultima pozitie pe care valoarea i a aparut, initializat cu 0. Cand suntem pe o pozitie$i$ iar lastOccurrence[v[i]] != 0, inseamna ca s-a format o pereche cu (lastOccurrence[v[i]]], i). Astfel, introducem in arborele de intervale valoarea i - lastOccurrence[v[i]] pe pozitia i, si tinem minte ca atunci cand ajungem cu L in dreptul pozitiei lastOccurrence[v[i]] + 1, vom seta pe 0 pozitia i din arborele de intervale. La final, in lastOccurrence[v[i]] se pune valoarea i. Se parcurg queryurile si se raspunde la ele.

Complexitate timp: O(NlogN).
Complexitate spatiu: O(N).

K. Padure2

Se observa ca numarul de moduri prin care se poate ajunge din (i1,j1) in (i2,j2) fara a baga in seama obstacolele este
Combinari(n, k) unde n = (i2 – i1) + (j2-j1), iar k = (i2-i1).
Stiind acest lucru putem defini o functie f(i1, j1, i2, j2) care calculeaza numarul de moduri prin care se poate ajunge din (i1,j1) in (i2,j2) fara a baga in seama obstacolele.
Sortam punctele in functie de diagonala secundara.
Fie un vector nr[i] = numarul de moduri prin care se poate ajunge din (1,1) in (l[i], c[i]), fara a trece printr-un obstacol.
Recurentapentru acest vector v-a fi:

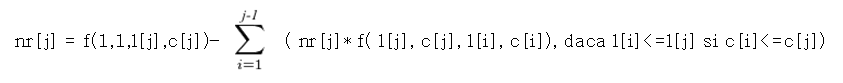
La final trebuie calculat dupa aceeasi regula pentru n,m.