| Fişierul intrare/ieşire: | impartiri.in, impartiri.out | Sursă | Infoarena Monthly 2012, Runda 6 |
| Autor | Vlad Ionescu | Adăugată de | |
| Timp execuţie pe test | 0.2 sec | Limită de memorie | 20480 kbytes |
| Scorul tău | N/A | Dificultate | N/A |
Vezi solutiile trimise | Statistici
Împărțiri
 Aceasta problema a fost sponsorizata de IXIA in runda 6! Participantul care a castigat premiul este Aceasta problema a fost sponsorizata de IXIA in runda 6! Participantul care a castigat premiul este |
Lui Marian ii plac foarte mult liniile, asa ca si-a desenat un dreptunghi in planul cartezian, avand coltul stanga-jos in punctul de coordonate (0, 0), iar coltul dreapta-sus in punctul de coordonate (N, M). El traseaza un numar de linii (posibil 0), insa cu urmatoarele proprietati:
- liniile sunt paralele fie cu axa Ox, fie cu axa Oy;
- liniile trec numai prin puncte de coordonate numere intregi;
- liniile trebuie sa intersecteze dreptunghiul dat intr-un numar finit si nenul de puncte;
- liniile trasate de Marian nu au voie sa se suprapuna, ci doar sa se intersecteze.
Dupa ce termina de trasat liniile, Marian observa ca dreptunghiul initial este divizat intr-un numar de dreptunghiuri mai mici.
Cerinţă
Determinati in cate moduri poate trasa Marian liniile cu proprietatile date, astfel incat aria fiecarui dreptunghi mai mic (din interiorul dreptunghiului initial) sa fie mai mica sau egala decat un numar natural K. Deoarece acest numar poate fi foarte mare, se cere doar restul impartirii sale la numarul 2113.
Date de intrare
Fişierul de intrare impartiri.in contine pe o singura linie 3 numere naturale: N, M si K, separate prin cate un spatiu, avand proprietatea din enunt.
Date de ieşire
În fişierul de ieşire impartiri.out se va afla pe prima linie un numar natural ce reprezinta numarul de moduri in care Marian poate trasa liniile astfel incat toate restrictiile sa fie respectate, modulo 2113.
Restricţii
- 2 ≤ N, M ≤ 3000
- 1 ≤ K ≤ N*M
- Linia este un segment cu lungimea infinita.
- Daca o linie se suprapune cu o latura a dreptunghiului, se considera ca linia intersecteaza dreptunghiul intr-o infinitate de puncte.
- Doua moduri de trasat linii se considera distincte daca la final (dupa ce se incheie procesul de trasare) continutul dreptunghiului initial este diferit.
Exemplu
| impartiri.in | impartiri.out |
|---|---|
| 3 2 2 | 4 |
Explicaţie
Modurile valide in care Marian poate trasa liniile sunt urmatoarele (cu albastru este reprezentat dreptunghiul initial, iar cu rosu liniile trasate):
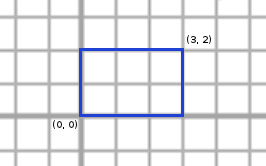
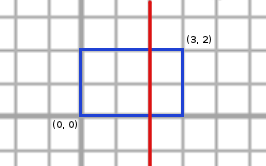
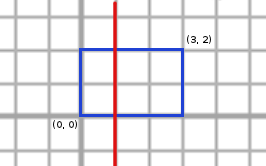
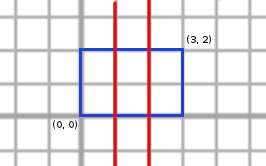
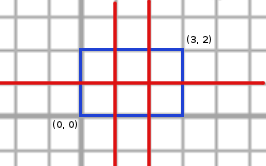
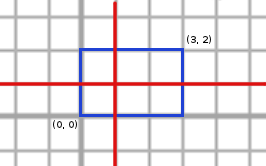
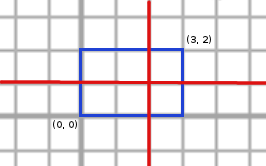
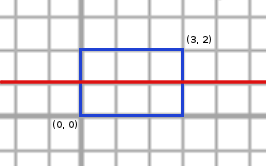
Din pacate, aria tuturor dreptunghiurilor din interiorul dreptunghiului initial trebuie sa fie cel mult 2 (caci K = 2), asa ca doar 4 moduri satisfac toate cerintele. Daca K ar fi fost egal cu 6, atunci raspunsul ar fi fost 8.
