Atenţie! Aceasta este o versiune veche a paginii, scrisă la 2008-02-18 17:18:00.
Revizia anterioară Revizia următoare

Notiuni elementare de geometrie si aplicatii

(Categoria Geometrie, Autori Savin Tiberiu si Sima Mihai Cotizo)

Drepte

Ecuatiile dreptei

Dreptele sunt locuri geometrice ce indeplinesc ecuatia dreptei. Cu alte cuvinte, ecuatia unei drepte reprezinta o relatie care este respectata de toate punctele aflate pe dreapta. Forma generala a ecuatiei unei drepte in sistemul xOy este

$(d): a*x + b*y + c = 0$

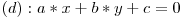
In cazul in care dreapta nu se afla in plan, fiecare punct A ( x1 , x2 , x3 ,... Xn ) (pentru n dimensiuni) de pe ea va indeplini conditiile:
$\left\{\begin{array}{lr} x_1 = x_0_1 + a_1; \ x_2 = x_0_2 + a_2; \ ... \ x_n = x_0_n + a_n; \end{array}\right$

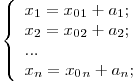
A nu se confunda cu ecuatia planului:

$(d): a*x + b*y + c*z + d = 0$

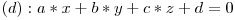
Feedback (Stefan): Ai cam incurcat treburile. Asta e ecuatia planului. :)
Edit (Cotizo): Fixed :)

Pentru simplitate, de aici inainte ne vom referi numai la drepte in plan. De mentionat este faptul ca daca trecem pe y in partea dreapta si impartim prin -b (consideram un caz general, nu cel nefericit in care b=0), obtinem:

$(d): y = \frac{(-a)}{b}*x + \frac{(-c)}{b}$

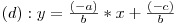
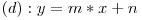$(d): y = m*x + n$ , unde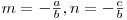 $m=-\frac{a}{b}, n=-\frac{c}{b}$

De asemenea, fiind date doua puncte A(x₁, y₁) si B(x₂, y₂), ecuatia dreptei determinate de ele se poate scrie

$(d): \frac{x-x_1}{x_2-x_1} = \frac{y-y_1}{y_2-y_1}$

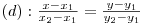
Aceasta poate sa nu ne fie de prea mare ajutor, dar facand produsul mezilor cu extremii si desfacand parantezele vom obtine 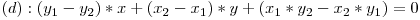$(d): (y_1-y_2)*x + (x_2-x_1)*y + (x_1*y_2-x_2*y_1) = 0$ , de unde putem deduce foarte usor cine sunt a, b, c din scrierile precedente.

Se stie ca orice dreapta imparte planul in 2 semiplane: cel cu puncte pentru care, daca aplicam ecuatia, vom obtine o valoare strict pozitiva, si cel pentru care vom obtine o valoare strict negativa. De aceea, daca avem o dreapta data prin 2 puncte A(x₁, y₁) si B(x₂, y₂) de pe aceasta, atunci punctul C(x₃, y₃) va apartine dreptei AB daca si numai daca

$\left| \begin{array}{ccc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{array} \right| = 0$

Feedback (Stefan): Pare destul de trivial/pueril/nefondat raspunsul la intrebarea "de ce toate ecuatiile sunt (in general) egale cu 0?". Se poate gasi o motivatie mai buna sau se poate renunta la ea.
Edit (Cotizo): Fixed, de asemenea... fac topic pentru articol si bag acolo sugestiile + TODO existent ?

Punctul de intersectie a 2 drepte

Dupa cum am vazut, o dreapta reprezinta un loc geometric. Sa zicem ca avem 2 drepte d₁ si d₂ si dorim sa aflam punctul A(x, y) cu propietatea ca acesta apartine atat dreptei d₁, cat si dreptei d₂. Scriem ecuatiile celor 2 drepte:

$a_1 * x + b_1 * y + c_1 = 0$
$a_2 * x + b_2 * y + c_2 = 0$

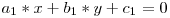
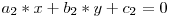
Am ajuns astfel la un sistem de 2 ecuatii cu 2 necunoscute. Pentru a ajunge la niste formule mai directe de calculare a celor 2 coordonate vom inmulti prima relatie cu b₂ si pe cea de-a doua cu b₁.

$a_1 * b_2 * x + b_1 * b_2 * y + c_1 * b_2 = 0$
$a_2 * b_1 * x + b_1 * b_2 * y + c_2 * b_1 = 0$

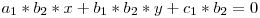
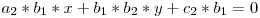
Scadem cele doua relatii si ajungem la o singura ecuatie cu o singura necunoscuta:

$(a_1 * b_2 - a_2 * b_1) * x + c_1 * b_2 - c_2 * b_1 = 0 \Leftrightarrow$
$x = \frac{c_2 * b_1 - c_1 * b_2}{a_1 * b_2 - a_2 * b_1}$

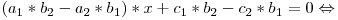
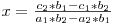
O data ce l-am aflat pe x, descoperirea celeilalte coordonate e destul de triviala:

$a_1*x + b_1 * y + c_1 = 0$
$y = \frac{-c_1 - a_1 * x}{b_1}$
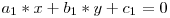
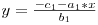
TODO: Fractiile arata prea mici cu LaTeX. Asta trebuie fixat cumva.

Panta unei drepte

Panta unei drepte se poate defini ca fiind tangenta unghiului facut de dreapta cu orizontala, mai exact cu orice dreapta paralela cu axa OX. Ea se calculeaza astfel:

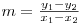$m = \frac{y_1-y_2}{x_1-x_2}$ sau $m = -\frac{a}{b}$

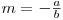
In a doua ecuatie a si b reprezinta coeficientii ecuatiei dreptei respective

$(d): a*x + b*y + c = 0$

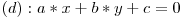
Proprietati:
• Doua drepte care au pantele egale sunt ori paralele ori confundate.
• Doua drepte care au produsul pantelor egal cu -1 sunt perpendiculare.

Distante

Distanta dintre 2 puncte

Consideram 2 puncte A(x₁,y₁) si B(x₂,y₂), si vrem sa aflam distanta dintre ele. Pentru a face acest lucru construim un al treilea punct C(x₂,y₁) si observam ca triunghiul ACB este dreptunghic iar distanta dintre punctele AB este intocmai ipotenuza acestui triunghi. Folosind teorema lui Pitagora ajunge la urmatoarea formula:

$d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$

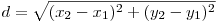
Distanta dintre un punct si o dreapta

Pentru a calcula distanta care ne trebuie noua vom calcula panta dreptei d₁ notata cu m₁. Acum vrem sa construim o dreapta d₂ perpendiculara pe dreapta d₁ care trece prin punctul A. Stim ca m₁*m₂=-1 si de aici aflam usor m₂ (panta dreptei d₂). In acest moment avem panta dreptei d₂ si un punct care ii apartine. Avand aceste 2 informatii putem sa calculam usor ecuatia ei si punctul de intersectie cu dreapta d₁ (Vezi capitolul Drepte). Distanta dintre dreapta si punct va fi egala cu distanta dintre punct si punctul de intersectie al celor 2 drepte.

De asemenea exista si o formula pt a determina distanta de la un punct la o dreapta: considerand punctul A(x,y) si dreapta d: ax+by+c=0, vom avea :

Distanta dintre un punct si un segment

Sa presupunem un punct A(x₁,y₁) si un segment determinat de punctele B(x₂,y₂) si C(x₃,y₃) si vrem sa aflam distanta dintre punct si segment.

D=min(dist(A,B),dist(A,C)) in cazul in care perpendiculara din punctul A pe dreapta BC nu cade in interiorul segmentului BC, altfel distanta va fi egala cu distanta dintre punctul A si dreapta BC, lucru care l-am tratat mai sus.

Arii

Aria unui triunghi

Aria unui triunghi determinat de punctele A(x₁,y₁), B(x₂,y₂) si C(x₃,y₃) este egala cu :

$A = \frac{1}{2} * abs \left( \left| \begin{array}{ccc} \ x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1\end{array} \right| \right)$

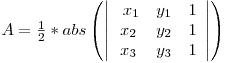
Unde abs(x) reprezinta valoarea absoluta a lui x. Determinantul de mai sus poate fi folosit si pentru a vedea daca cele 3 puncte sunt in sens invers sau direct trigonometric, el fiind negativ in cazul in care punctele sunt in sens invers trigonometric.

Aria unui poligon

Aria unui poligon convex cu n laturi o putem calcula foarte usor folosind formula pentru aria unui triunghi astfel.

$\displaystyle \sum_{i=2}^{i<n} Arie(p_{1},p_{i},p_{i+1})$

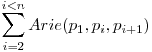
Unde 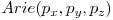$Arie(p_{x},p_{y},p_{z})$ reprezinta aria triunghiului determinat de punctele p_x, p_y, p_z.

Aria unui poligon concav se calculeaza la fel doar ca atunci cand calculam 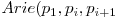$Arie(p_{1},p_{i},p_{i+1}$ renuntam la abs, si tinem minte semnul determinantului si luam valoarea absoluta dupa ce am calculat intreaga suma.

Probleme rezolvate

Infasuratoarea convexa

Enuntul problemei: Se da un set de puncte in plan, sa se determine un poligon convex de arie minima care contine toate punctele in interiorul sau.
Rezolvare: O posibila solutie este sa fixam punctul cu abscisa minima si sa translatam toate punctele pana cand acesta ajunge in punctul de coordonate (0,0). Acum vom sorta punctele dupa formula 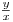$\frac{y}{x}$ unde x si y sunt coordonatele punctului, iar in caz de egalitate dupa distanta fata de punctul (0,0). In cazul nefericit in care x=0 vom considera ca 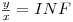$\frac{y}{x} = INF$ . Apoi vom parcurge punctele in ordine si le vom introduce intr-o stiva. Inainte sa introducem un punct in stiva trebuie insa sa ne uitam daca nu cumva punctele st[vf-1] , st[vf] si P sunt in ordine invers trigonometrica ( st - stiva, vf - varful stivei, P - punctul curent). Aici ne vom folosi de o alta proprietate a determinantului cu ajutorul caruia determinam aria unui triunghi. Mai exact vom calcula
$D=\left| \begin{array}{ccc} \ x_1 & y_1 & 1\ x_2 & y_2 & 1\ x_3 & y_3 & 1\end{array} \right|$
pentru st[vf-1] = (x₁.y₁) , st[vf]= (x₂,y₃), P(x₃,y₃). Daca D este negativ atunci inseamna ca unghiul cu originea in st[vf] face o intoarcere la dreapta si trebuie scos din stiva. Repetam procedeul pana cand ramanem cu un singur punct in stiva sau pana cand intalnim un D >= 0 dupa care adaugam punctul in stiva. Dupa ce am terminat e posibil ca poligonul nostru inca sa fie convex deoarece nu am verificat unghiul care are originea in st[vf], asa ca il vom calcula pe D pentru punctele st[vf-1],st[vf],st[ 1 ] si vom scoate punctul din varf atata timp cat D va fi negativ. Punctele ramase reprezinta infasuratoarea convexa a setului de puncte primite la intrare.

Feedback (Stefan): Articolul trebuie imbracat intr-o forma mai prezentabila. Nu trebuie sa ramana doar o lista de formule si schelete de probleme. De asemenea, trebuie compactat si eliminate spatiile mari care il fac greu de citit.
TODO: Adaugati si centru de greutate a unui poligon si eventual explicati de ce merge formula de mai sus pt aria unui poligon concav.

sugestii de probleme de adaugat

punct in poligon:
- punct in triunghi
- punct in poligon oarecare
- punct in poligon convex 2 solutii cautare binara dupa unghi sau dupa y
- punct in poligon stelat
- problema poligon din arhiva

infasuratoare convexa X
vreo 5 metode

gasire rapida a celui mai de sus punct din un poligon convex

determinare daca un poligon e convex sau concav

determinare a sensului de parcurgere a varfurilor unui poligon

intersectii de drepte cu un poligon convex

rotating calipers
- perechea de puncte cele mai departate
- dreptunghiul de arie minima ce contine un set de puncte

halplane intersection

infoarena informatica de performanta