Soluţii Grigore Moisil 2010

Lista de probleme
Pătrat2
Telefon
G2
Joc14
Magic2
Pietre2
Egipt
Inv
CCM
Transport2

Patrat2

Vom genera pătrate mai mici decât n. În algoritm, ieşim din structura când condiţia i * i < n nu mai este îndeplinită. În acest caz, dacă i * i este mai mare decât n, scădem din i valoarea 1 pentru a avea un pătrat care „încape” în n, îl scriem în fişier şi scădem din n pătratul aferent. Repetăm aceşti paşi până când n devine 0.

Algoritm Patrat(n):
  cât timp n > 0 execută:
    i = 1
    cât timp i * i < n execută:
      i = i + 1
    sfârşit (cât timp)
    dacă i * i > n atunci
      i = i – 1
    sfârşit(dacă)
    Scrie i
    n = n – i * i
  sfârşit (cât timp)
Sfârşit (algoritm)

Telefon

Cum numărul de telefon se va prelucra pe cifre de la stânga la dreapta, este mai avantajos să-l citim sub forma unui şir de caractere. În paralel reţinem şi lungimea numărului în n. Şirul de comenzi îl păstrăm tot într-un şir de caractere.
Vom genera separat prima mutare de deasupra butonului * deasupra primului buton dorit. La fel, ultima mutare implică altfel de comenzi, deoarece trebuie să ajungem de deasupra unui buton oarecare deasupra butonului #.
În rest, presupunem că ne aflăm deasupra unui buton oarecare cu o cifră c1 şi trebuie să ne mutăm deasupra unui buton cu o altă cifră c2. Programul se ramifică în funcţie de c1 în 10 cazuri şi pentru fiecare valoare posibilă a lui c1 din nou în 10 cazuri acoperind valorile posibile ale lui c2. Vom fi atenţi ca în cazul în care trebuie să efectuăm doi paşi, să începem cu mutarea pe verticală. Mutările se pot grupa după caz, observând că, de exemplu, atunci când ne aflăm pe o anumită linie (de exemplu, 1 2 3) şi trebuie să ajungem pe o altă linie (de exemplu, 4 5 6) pentru întreaga linie mai întâi mutarea va fi J 1.
Alt caz particular este când două cifre consecutive în numărul de telefon sunt identice, caz în care se repetă comanda A.

G2

Vom folosi metoda greedy. În realitate însă nu este nevoie decât de puţină intuiţie. Condiţia ca produsul cifrelor să fie n ne conduce la ideea că cifrele numărului sunt divizori ai lui n. Un cel mai mic număr presupune în primul rând un număr minim de cifre. Astfel, vom descompune pe n într-un produs de cât mai mulţi de 9, după care cât mai mulţi de 8... până la 2. Numărul căutat reprezintă numărul format cu aceste cifre în ordine crescătoare.

Joc14

Simularea, în orice situaţie înseamnă organizarea paşilor şi alegerea reprezentării. Vom avea, la fiecare pas, două tablouri ( tnou şi tvechi) care se completează cu caractere '.'. Apoi, în ambele tablouri aşezăm litera 'o' (sau cele două litere 'o') pe poziţiile date în fişierul de intrare.
La fiecare pas efectuăm, pe baza regulilor date, mutările jocului până când o literă 'o' ajunge pe marginea caroiajului. Rezultatul mutării o generăm în tnou, iar după mutare copiem tnou în tvechi, urmând să lucrăm la următoarea mutare pe baza acestuia.
În algoritmul mutării vom căuta poziţia unui caracter '.', pentru a-i număra vecinii pe care se află un caracter 'o' sau ' * ' .Dacă numărul acestora este 1, reţinem poziţia caracterului '.', respectiv pentru a suprascrie acest caracter cu litera 'o'. Ştiind că pe marginea exterioară a figurii putem avea doar caractere 'o', reţinem faptul, după caz, că s-a terminat jocul. Urmează să suprascriem caracterele 'o' cu ' * ' şi caracterele '*' cu '.' .

Magic2

Problema poate fi abordată în multe feluri. În principiu se realizează un algoritm naiv dar care impune atenţie deosebită.
În algoritm vom trata următoarele trei cazuri:

Tabloul este magic
Cele două elemente se află pe linii şi coloane diferite
Cele două elemente se află pe aceeaşi linie
Cele două elemente se află pe aceeaşi coloană

Pentru oricare din posibilele tablouri trebuie determinată suma magică. Nu este banal, deoarece nu cunoaştem linia, respectiv coloana greşită. Deci, se determină toate sumele liniilor şi se păstrează ca sumă magică, cea care apare cel puţin de trei ori (cel mult două linii pot fi greşite). Dacă nu găsim nicio linie greşită, rezultă că pătratul este magic (coloanele nu trebuie verificate, deoarece dacă nu am găsit nicio linie eronată, rezultă că şi coloanele sunt corecte).
Dacă nu găsim două linii greşite, rezultă că cele două elemente eronate se află pe aceeaşi linie. Pentru liniile găsite greşite păstrăm indicele şi suma lor. Vom proceda similar şi în cazul coloanelor.
Urmează determinarea diferenţiată după cele trei cazuri de mai sus a valorilor corecte.

Pietre2

Soluţie 1

Rezolvarea se bazează pe observaţia că dacă vom procesa înălţimile în ordine crescătoare, atunci vom putea actualiza un drum de lungime maximă ce se termină în fiecare din aceste pătrăţele în mod corect.

Astfel, algoritmul va sorta crescător toate cele n² pătrăţelele :

Algoritm Rezolvă(n):
  pentru fiecare (h, i, j) execută:	// pătrăţelul (i, j) cu înălţimea h
    pentru fiecare vecin (h’, i’, j’) cu h = h’ + 1 execută:
	dacă lg[i][j] < lg[i’][j’] + 1 atunci
	  lg[i][j] = lg[i’][j’] + 1
	sfârşit(dacă)
    sfârşit(pentru)
  sfârşit(pentru)

   caută max{lg[i][j] : 1 <= i, j <= n}
  reconstruieşte drumul alegând un vecin cu lungimea mai mică cu exact 1 
  până ce se ajunge la marginea matricei.
Sfârşit(algoritm)

În implementare se va ţine cont ca pătrăţelele de pe marginea matricei care sunt puncte de plecare să fie marcate iniţial cu 0.
Complexitate: O(N² log(N)).

Soluţie 2

Problema, în ciuda faptului că limita pentru n este mare, se putea aborda şi cu backtracking. Cu o rezolvare asemănătoare cu cea de mai jos se putea obţine 90 puncte.
În programul principal:

Algoritm Pietre(n,t): 	// n: dimensiunea tabloului t 
  max = 0	// lungimea maximă a drumului 
  maxlin = 0 	// linia de unde porneşte cel mai lung drum 
  maxcol = 0	// coloana de unde porneşte cel mai lung drum 
  lin = 1 	// vom încerca să intrăm în tablou pornind din linia 1 
  pentru col=1,n execută:
    maxnou = 0 	// maximul actual 
    rez[lin,col] = 1 	// marcăm punctul de pornire 
    cauta(lin,col,2) 	// căutăm un drum având acest punct de start 
    dacă maxnou > max atunci	// actualizarea 
      max = maxnou
      maxlin = lin
      maxcol = col
    sfârşit(dacă)
  sfârşit(pentru)
  //...  	 la fel procedăm cu linia n, coloana 1 şi coloana n 
sfârşit(algoritm)

Algoritm Cauta(lin,col,pas):
  pentru i=1,4 execută:	// un element are 4 vecini 
    lin_nou = lin + x[i] 	// indicele de linie al vecinului 
    col_nou = col + y[i]	// indicele de coloană 
	// dacă am generat o poziţie pe teren }
    dacă (lin_nou = {1,2,...,n}) şi (col_nou = {1,2,...,n}) atunci
      dacă rez[lin_nou,col_nou] = 0 atunci 	// dacă nu am fost aici 
	// dacă numărul pietrelor este cu 1 mai mare 
        dacă t[lin_nou,col_nou] = t[lin,col] + 1 atunci
          rez[lin_nou,col_nou] = pas	// facem pasul 
          dacă pas > maxnou atunci    	 //actualizăm maximul actual
            maxnou = pas
          sfârşit(dacă)
          Cauta(lin_nou,col_nou,pas+1) 	// încercăm să continuăm drumul 
          rez[lin_nou,col_nou] = 0	// ştergem pasul, pentru că vom căuta alt drum 
        sfârşit(dacă)
      sfârşit(dacă)
    sfârşit(dacă)
  sfârşit(pentru)
Sfârşit(algoritm)

unde şirurile x şi y au valorile:
x = (-1,0,1,0)
y = (0,1,0,-1)

Soluţie 3
Problema se poate rezolva şi în complexitatea O(N²) folosind memoizarea. Astfel, vom calcula pentru fiecare element al matricii cât se poate urca dacă pornim din elementul respectiv. Pseudocodul funcţiei care calculează pentru fiecare element cât se poate urca dacă pornim din elementul respectiv arată astfel:

funcţie din(i, j):
  dacă(D[i][j] != 0) atunci 
    returnează D[i][j]
  sfârşit dacă

  D[i][j] = 1

  pentru fiecare vecin (i’, j’) al perechii (i, j) execută:
    dacă A[i][j] + 1 = A[i’][j’] şi D[i][j] < din(i’, j’) + 1 atunci
      D[i][j] = din(i’, j’) + 1
    sfârşit dacă
  sfârşit pentru
Sfârşit(din)

Se observă că fiecare pentru fiecare element al matricii, funcţia este apelată de un număr constant de ori, deci complexitatea algoritmului este O(N²).

Egipt

Soluţie 1

Fie n1 numărul elementelor egale cu 1, n2 numărul elementelor egale cu 2 şi n3 numărul elementelor egale cu 3 în şirul dat a. Altfel spus, în şirul ordonat vom avea valori egale cu 1 începând cu poziţia 1 până la poziţia n1, valori egale cu 2 începând cu poziţia n1+1 până la poziţia n1+n2, după care vom avea elemente egale cu 3.
Notăm cu m_ij numărul elementelor egale cu j care se află pe o poziţie pe care ar trebui să avem valoarea i. (Matricea m are 3 linii şi 3 coloane.)

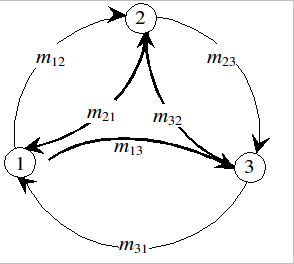
Fig. 1. În mij avem numărul elementelor care trebuie duse de pe poziţia i pe poziţia j
Observăm că
m₁₂ + m₁₃ = m₂₁ + m₃₁
m₂₁ + m₂₃ = m₁₂ + m₃₂
m₃₁ + m₃₂ = m₁₃ + m₂₃

Dacă avem 2 pe poziţia unui 1 şi 1 pe poziţia unui 2, avem nevoie de o singură interschimbare.
Dacă avem o configuraţie 2 3 1, sau 3 1 2, avem nevoie de două interschimbări.

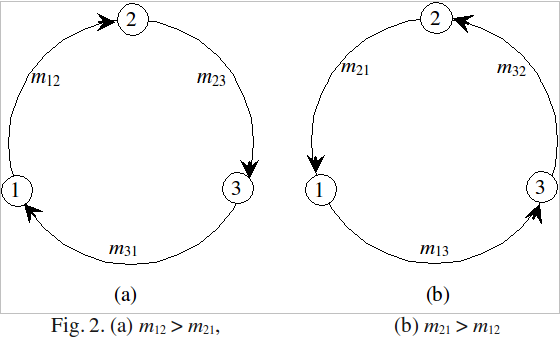
Rezultă că numărul minim de interschimbări care sunt necesare pentru ordonarea şirului este:
min(m₁₂, m₂₁) + min(m₂₃, m₃₂) + min(m₁₃, m₃₁) + 2|m₁₂ − m₂₁|
Realizarea interschimbărilor:

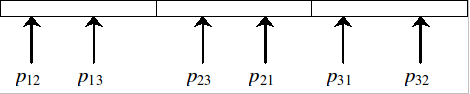
Fig. 3. Poziţiile interschimbărilor: p_ij este indicele elementului egal cu j aflat pe poziţia i

Soluţie 2

Rezolvarea se face în două faze. În prima fază vom pune la loc elementele egale cu 1. Pornim cu trei variabile: i va itera pornind din prima poziţie şi va merge până în ultima poziţie unde trebuie să ajungă un element egal cu 1; i2 va porni din prima poziţie unde trebuie să ajungă un element egal cu 2 şi va merge pâna la ultima poziţie de acest fel; similar i3 va itera pe intervalul unde trebuie să ajungă elementele egale cu 3.
i2 şi i3 vor fi poziţionate întotdeauna asupra unui element egal cu 1. Dacă elementul pe care am poziţionat i este egal cu 1, nu trebuie să facem nimica, doar incrementăm i. Dacă acesta este egal cu 2, vom schimba elementele de pe locurile i şi i2 şi vom incrementa i, iar pe i2 îl poziţionăm pe următorul element egal cu 1. Dacă cu i2 am depăşit pragul din dreapta al intervalului (adică ultimul loc unde trebuie să ajungă 2), elementul de pe poziţia i îl vom schimba cu elementul arătat de i3. Procedăm similar pentru elementele egale cu 3.
În a doua fază vor ajunge şi elementele egale cu 2 şi 3 la locul lor, prin interschimbări evidente.

Inv

Soluţie 1
Problema se poate rezolva în complexitate O(n*log(n)) şi cu ajutorul unei structuri de date tip Arbori Indexaţi Binar, sau Arbori de Intervale. În primul pas vom normaliza şirul din input, adică vom asocia fiecărui număr din şir un număr între 1 şi n astfel încât ordinea relativă a elementelor să rămână neschimbată. Normalizarea se face printr-o sortare a şirului iniţial dacă avem elemente care nu sunt egale sortăm crescător după valoarea lor iar dacă sunt egale sortăm crescator dupa indicele din şirul original.
După ce am obţinut şirul normalizat, îl parcurgem de la stânga la dreapta şi pentru fiecare element: interogăm câte elemente cu indice strict mai mari ca el am introdus în arbore( din acest motiv daca avem valori egale trebuie sa le avem in ordinea crescatoare a pozitiilor pentru ca altfel vom numara si elemenetele cu valoare egala cu cel actual introduse in structura de date) , incrementăm soluţia cu acest număr, după care introducem şi elementul actual în arbore.

Soluţie 2
Întrucât structurile de date menţionate anterior depăşesc nivelul clasei a 10-a, vom prezenta o soluţie ce se bazează pe tehnica divide et impera. La fiecare pas vom împărţi şirul în 2 părţi şi vom aplica algoritmul Merge Sort cu o mică modificare. Când interclasăm cele două bucăţi, reţinem şi bucata în care erau elementele (dacă erau în stânga sau în dreapta). Astfel, pentru fiecare element din partea stângă vom adăuga la soluţie câte elemente din dreapta se află în faţa lui după interclasare, lucru care se poate realiza în timp liniar. Cum adâncimea recursiei este logN, complexitatea finală este O(N logN).

Ccm

Problema se rezolvă utilizând metoda programării dinamice. Stările se vor determina urmând observaţia... Va trebui să cuplăm cele n noduri din mulţimea L cu unele noduri din mulţimea R, reprezentate de biţii de 1 din întregul stare. Fie, astfel, $bst[i][stare]$ valoarea maximă a cuplajului dintre primele i noduri din L şi nodurile din stare iar $ccm[i][stare]$ câte cuplaje de cardinalitate maximă există.
Recurenţa este:
$ccm[i][stare] = ccm[i - 1][stare] + \displaystyle\sum_{j \in V(i)}\ {ccm[i-1][stare-2^j]}$
Considerăm în continuare nodurile din R reţinute de stare ca nodurile actuale din R. Astfel, fie vom cupla primele i – 1 noduri cu nodurile reţinute de stare din R, fie vom încerca să cuplăm nodul i cu unul din nodurile din R actuale vecine cu acesta. Fie j acest nod. Acum ne rămân de cuplat primele i – 1 noduri din L cu nodurile stare – 2^j din R.
Valorile matricei $ccm[i][stare]$ se vor actualiza corespunzător în funcţie de valoarea lui $bst[i][stare]$ .
Complexitate: O(2ⁿ * n * m).

Transport2

Soluţie 1
Pentru a afla costul de la nodul 1 la nodul N, vom utiliza algorimul lui Dijkstra puţin modificat. Astfel, vom reţine pentru fiecare nod, valoarea minimă între nodul 1 şi nodul respectiv. Când dorim să mergem în vecinii nodului curent trebuie verificat dacă min(costul_nodului_curent, costul_muchiei) > costul_nodului_vecin. Complexitatea acestui algoritm este O(M logN).

Soluţie 2
Vom căuta binar răspunsul între 1 şi valoarea maximă pe care o poate avea o muchie. Pentru o valoare fixată, vom considera doar muchiile cu valoarea mai mare sau egală cu valoarea fixată şi vom utiliza o parcurgere în adâncime pentru a vedea dacă nodurile 1 şi N sunt în aceeaşi componentă conexă. Complexitatea acestei soluţii este O((N + M)*log MaxVal).

Soluţie 3
Pentru fiecare valoare vom reţine ce muchii au valoarea respectivă. Apoi, vom itera prin toate valorile posibile începând de la cea maximă şi la fiecare pas vom uni nodurile care sunt legate prin muchia respectivă folosind structura mulţimi disjuncte. Ne vom opri în momentul în care nodurile 1 şi N sunt în aceeaşi componentă conexă, rezultatul fiind prima valoare pentru care nodurile 1 şi N se află în aceeaşi componentă conexă. Complexitatea acestei soluţii este O(M log*N).