Square root trick

Cosmin Negruseri
20 iulie 2012

....
Being flexible and easy to code, this trick is pretty popular among the Romanian programming contests community.

Let’s check out a few problems.
Range Sum

Given an n elements array, implement a data structure for point updates and range sum queries:
- set(i, x): a[i] := k,
- sum(lo, hi) returns a[lo] + a[lo+1] + .. + a[hi].

The naive solution uses an array. It takes 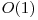time for an update and 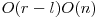for the range sum.

A more efficient solution splits the array into length k slices and stores the slice sums in an array S.

The update takes constant time.

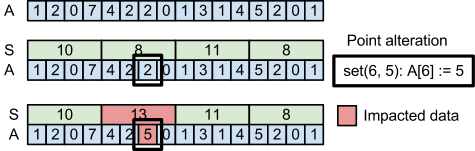
S[i/k] = S[i/k] - A[i] + x
A[i] = x

The range sum query is interesting. Slices completely contained in our range are summed up fast. The elements of the first and last slice (partially contained in the queried range) have to be traversed one by one.

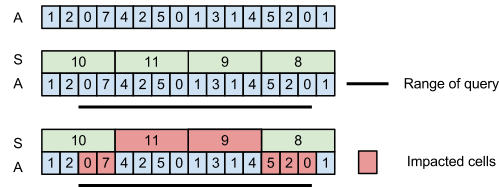
i = l
while i % k != 0 and i < r:
  sum += a[i]
  lo += 1
while i + k < r:
   lo += k
   sum += s[lo/k]
while lo + 1 <= r:
   lo += 1
   sum += a[lo]

The query takes less than time. 2k + n/k is minimized when k ~ sqrt(n). For k = sqrt(n) the query takes O(sqrt(n)) time.

This trick also works for other associative operations, like: min, gcd, product etc.

Nearest neighbour

Given a set S of n points and a query point p, find the point in S closest to p.

For uniformly distributed points, a good strategy is to represent the space as a grid and maintain a list of inner points for each cell. For a given query point, we can check the cell the point falls into and its neighbouring cells. For a sqrt(n) * sqrt(n) grid we’ll have one point per cell, on average. So, on average, finding the point in S closest to p, requires traversing a constant number of cells.
Longest common subsequence solution

Given two strings A (n characters) and B (m characters), find their longest common subsequence. (eg. The longest common sub sequence for abcabc and abcbcca is abcbc.)

There is a standard dynamic programming solution which uses an array best[i][j] to mean the longest common sub sequence for A[0:i] and B[0:j], computed as below:

if A[i] == B[j]:
   best[i][j] = 1 + best[i - 1][j - 1]
else:
  best[i][j] = max(best[i-1][j], best[i][j-1])

This algorithm takes O(nm) time and only O(n) space, since to compute a row you just need the previous row.
If you must return the actual sub sequence this doesn't work. You can keep an array of parent pointers, so that for each state (i, j) you know the previous state in the solution. The longest sub sequence corresponds to a path from (n-1, m-1) to (0, 0) on the parent matrix. This solution takes O(nm) space.

Let's see how can we use less memory.
We solve the problem once and save every kth row from the best matrix and from the parent matrix.
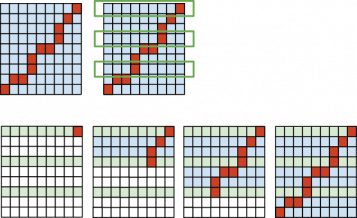We can start from the last saved row to n to compute the solution path from the n - 1 line to [n/k] * k line. And then go lower and lower to compute the part of the solution between the ik (i+1)k. Computing part of the path between row ik and row (i+1)k takes k * m space and k * m time. Computing the whole path takes n/k * (k * m) = nm time and km space, keeping every kth row in memory takes [n/k]m. again we minimize memory by using k = sqrt n

Caveats
The above problems have better solutions using interval trees or some other clever tricks. The sqrt trick is nice, since it improves the naive solution a lot without much effort.

Additional problems

1. (Josephus problem) n people numbered from 1 to n sit in a circle and play a game. Starting from the first person and every kth person is eliminated. Write an algorithm that prints out the order in which people are eliminated.
2. (Level ancestor) You are given an tree of size n. ancestor(node, levelsUp) finds the node’s ancestor that is levelsUp steps up. For example, ancestor(node, 1) returns the father and ancestor(node, 2) returns the grandfather. Implement ancestor(node, levelsUp) efficiently. (O(sqrt(n)) per query)
3. (Range median) You are given an array of size n. Implement a data structure to perform update operations a[i] = k and range median operations efficiently. The range median query, median(l, r) returns the median element of the sorted subsequence a[l..r]. ($O(\log n)$ per update and O(sqrt n log n) per query)

You can discuss the problems in the comments section.

4. Compute the number of digits of n!.
5. 2 balls